（本小題12分）
已知關于坐標軸對稱的橢圓經過兩點A（0，2）和B
.
（1）求橢圓的標準方程
（2）若點P是橢圓上的一點，F1和F2是焦點，且∠F1PF2=30°,求△F1PF2的面積.
（1）設經過兩點A（0，2），B
的橢圓標準方程為
mx2+ny2=1，代入A、B得
，
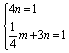
∴所求橢圓方程為
. ………5分
（2）在橢圓中，a=2,b=1.∴c=
=
又∵點P在橢圓上，∴|PF1|+|PF2|=2a=4. ①………6分
由余弦定理知：|PF1|2+|PF2|2-2|PF1||PF2|cos30°=|F1F2|2=(2c)2=12. ………8分 ②
把①兩邊平方得|PF1|2+|PF2|2+2|PF1|·|PF2|=16， ③
③-②得（2+
）|PF1|·|PF2|=4，
∴|PF1|·|PF2|=4（2-）， ………10分
∴
=
|PF1|·|PF2|sin30°=2-. ………12分
快樂暑假暑假能力自測中西書局系列答案科目：高中數學 來源：2010-2011學年福建師大附中高三上學期期中考試理科數學卷 題型：解答題
（本小題12分）已知函數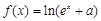
（
為常數）是實數集
上的奇函數，函數
是區間[－1，1]上的減函數．
（I）求的值；
（II）若
在
及
所在的取值范圍上恒成立，求
的取值范圍；
（Ⅲ）討論關于
的方程
的根的個數．
查看答案和解析>>
科目：高中數學 來源：2010年吉林省高一上學期期中考試數學試卷 題型：解答題
（本小題12分）已知二次函數
滿足
且
．
（1）求的解析式；
(2) 當
時，不等式：
恒成立，求實數
的范圍．
（3）設
，求
的最大值；
查看答案和解析>>
科目：高中數學 來源：2010-2011年福建省高二下學期期中考試理科數學 題型：解答題
（本小題12分）
已知雙曲線的中心在原點，左右焦點分別為
，離心率為
，且過點
，
（1）求此雙曲線的標準方程；
（2）若直線系
（其中
為參數）所過的定點
恰在雙曲線上，求證：
。
查看答案和解析>>
科目：高中數學 來源：2010-2011年福建省四地六校高二下學期第一次月考數學文卷 題型：解答題
（本小題12分）
已知橢圓C的左右焦點坐標分別是（－1，0），（1， 0），離心率
，直線
與橢圓C交于不同的兩點M，N，以線段MN為直徑作圓P。
（1）求橢圓C的方程；
（2）若圓P恰過坐標原點，求圓P的方程；
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
直線
，且直線
與曲線
相切于點
，求直線
的坐標。