
(本題滿分11分)在△ABC中,內角A,B,C對邊的邊長分別是a,b,c,已知c=2,C= .
.
(1)若△ABC的面積等于 ,求a,b;
,求a,b;
(2)若sinC+sin(B-A)=2sin2A,求△ABC的面積.
(1)a=2,b=2.(2)S=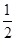 absinC=
absinC=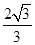 .
.
解析試題分析:(1)由余弦定理及已知條件得,a2+b2-ab=4,…………2分
又因為△ABC的面積等于 ,所以
,所以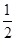 absinC=
absinC= ,得ab=4.…………4分
,得ab=4.…………4分
聯立方程組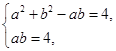 解得a=2,b=2.…………5分
解得a=2,b=2.…………5分
(2)由題意得sin(B+A)+sin(B-A)=4sinAcosA,即sinBcosA=2sinAcosA,…………7分
當cosA=0時,A= ,B=
,B=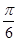 ,a=
,a= ,b=
,b=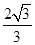 ,…………8分
,…………8分
當cosA≠0時,得sinB=2sinA,由正弦定理得b=2a,聯立方程組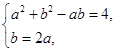
解得a=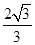 ,b=
,b= .…………10分
.…………10分
所以△ABC的面積S=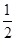 absinC=
absinC=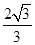 .…………11分
.…………11分
考點:本題主要考查正弦定理、余弦定理的應用,三角形內角和定理,兩角和差的三角函數。
點評:典型題,本題在考查正弦定理、余弦定理的應用,三角形內角和定理,兩角和差的三角函數的同時,考查了函數方程思想,在兩道小題中,均通過建立方程組,以便求的a,b,c等。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
某興趣小組測量電視塔AE的高度H(單位:m),如示意圖,垂直放置的標桿BC的高度h=4m,仰角∠ABE= ,∠ADE=
,∠ADE= 。
。
(1) 該小組已經測得一組 、
、 的值,tan
的值,tan =1.24,tan
=1.24,tan =1.20,請據此算出H的值;
=1.20,請據此算出H的值;
(2) 該小組分析若干測得的數據后,認為適當調整標桿到電視塔的距離d(單位:m),使 與
與 之差較大,可以提高測量精確度。若電視塔的實際高度為125m,試問d為多少時,
之差較大,可以提高測量精確度。若電視塔的實際高度為125m,試問d為多少時,

 最大?
最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com