中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

（本小題滿分12分）
在中，角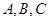所對的邊分別為，且滿足．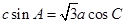
（1）求角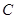的大小；
（2）求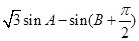的最大值，并求取得最大值時角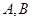的大小．

（1）（2）最大值為1，此時

解析試題分析：（1）由結合正弦定理得，
，                                             ……2分
從而，，                                    ……4分
∵，∴；                                              ……6分
（2）由（1）知，                                           ……7分
∴                               ……8分

                                 ……9分
，                                    ……10分
∵，∴，
當時，取得最大值，                    ……11分
此時．                                                 ……12分
考點：本小題主要考查正弦定理，余弦定理，三角函數的化簡和三角函數的圖象和性質.
點評：高考中經常將三角函數和向量結合正弦定理、余弦定理出題考查，難度一般不大，但是三角函數中公式比較多，要牢固掌握，靈活選擇應用，還要注意各個公式的適用條件.

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：解答題

的三個內角對應的三條邊長分別是,且滿足
（1）求的值；
（2）若, ，求和的值.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

已知A、B、C是三角形ABC的三內角，且
，并且
（1）求角A的大小。
（2）的遞增區間。

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

已ΔABC的內角A,B，C對的邊分別為a,b,c =" (2a,C" -26) , = (cosC,l)，且丄.
(I)求角A的大小;
(II )若a = 1,求b +c的取值范圍.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題


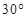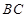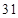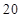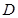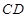如圖所示，港口北偏東方向的點處有一觀測站，港口正東方向的處有一輪船，測得為海里.該輪船從處沿正西方向航行海里后到達處，測得為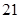海里. 問此時輪船離港口還有多少海里?

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

中，角A，B,C的對邊分別是且滿足
（1）求角B的大小；
（2）若的面積為為且，求的值；

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

平面直角坐標系中有一個△ABC，角A,B,C所對應的邊分別為，已知坐標原點與頂點B重合，且,,=，且∠A為銳角。（12分）
(1)求角A的大小；
(2)若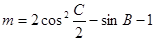，求實數的取值范圍；
(3)若，頂點A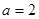，，求△ABC的面積。

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

（本題滿分12分）在中，角所對的邊分別為a,b, c．
已知且．
（Ⅰ）當時，求的值；
（Ⅱ）若角為銳角，求p的取值范圍

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

(本題滿分11分)在△ABC中，內角A，B，C對邊的邊長分別是a，b，c，已知c＝2，C＝.
（1）若△ABC的面積等于，求a，b；
（2）若sinC＋sin(B－A)＝2sin2A，求△ABC的面積．

查看答案和解析>>

同步練習冊答案