
在△ABC中,a、b、c分別為角A、B、C所對的邊,且
(2b+c)cosA+acosC =0
(1)求角A的大小:
(2)求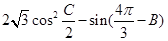 的最大值,并求取得最大值時角 B.C的大小.
的最大值,并求取得最大值時角 B.C的大小.
(1) ;(2)
;(2) 
解析試題分析::(1)此類解三角形的問題,主要使用正余弦定理,將邊角互化,對于第一問,通過觀察,利用余弦定理,可將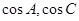 化簡,轉化成邊的關系,然后利用
化簡,轉化成邊的關系,然后利用 ,得到角A的大小;
,得到角A的大小;
(2)通過公式 ,將角
,將角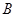 轉化成角
轉化成角 ,利用兩角和的正弦公式展開,化一,得到原式
,利用兩角和的正弦公式展開,化一,得到原式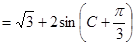 ,根據角
,根據角 的范圍,結合三角函數的圖像,當
的范圍,結合三角函數的圖像,當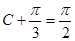 時,取得最大值,得到此時的角
時,取得最大值,得到此時的角 的大小,此題屬于基礎題型.
的大小,此題屬于基礎題型.
試題解析:(1)法一: ?
? ,
,
由正弦定理,得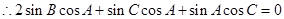 2分
2分
即 ,
, , 4分
, 4分
在 中,
中,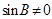 ,
,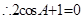 ,即
,即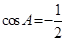 ?又
?又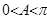 ,所以
,所以 6分
6分
??法二:  ?
?
所以由余弦定理得, 2分??
2分??
化簡整理得 ,由余弦定理得
,由余弦定理得 ?? 4分
?? 4分
所以 ,即
,即 ?又
?又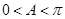 ?所以
?所以 ? 6分
? 6分
(2)∵ ,∴
,∴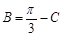 ,
, .
.
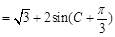 8分
8分
∵ ,∴
,∴ ,∴當
,∴當 ,
, 取最大值
取最大值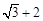 ,此時
,此時 . 12分
. 12分
考點:三角函數的化簡與求值


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com