
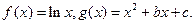
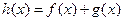 是單調遞增函數,求實數
是單調遞增函數,求實數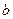 的取值范圍;
的取值范圍;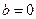 時,兩曲線
時,兩曲線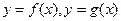 有公共點P,設曲線
有公共點P,設曲線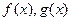 在P處的切線分別為
在P處的切線分別為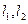 ,若切線
,若切線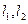 與
與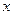 軸圍成一個等腰三角形,求P點坐標和
軸圍成一個等腰三角形,求P點坐標和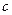 的值;
的值;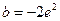 時,討論關于
時,討論關于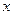 的方程
的方程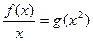 的根的個數
的根的個數
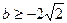 (2)
(2)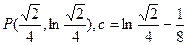
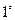
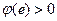 即
即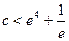 時,函數
時,函數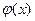 有兩個零點即方程
有兩個零點即方程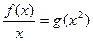 有兩個根;
有兩個根;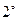
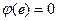 即
即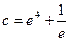 時,函數
時,函數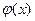 有一個零點即方程
有一個零點即方程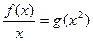 有一個根;
有一個根;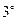
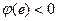 即
即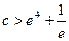 時,函數
時,函數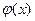 沒有零點即方程
沒有零點即方程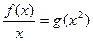 沒有根
沒有根
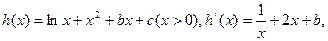
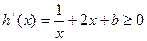 在
在 上恒成立,
上恒成立,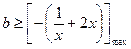 ,又
,又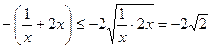 (當且僅當
(當且僅當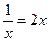 ,即
,即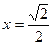 時取等)∴
時取等)∴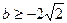 .
.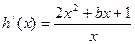 ,令
,令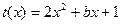 ,則
,則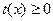 在
在 上恒成立,
上恒成立,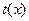 圖象得,
圖象得,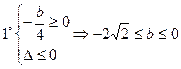 ;
;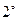
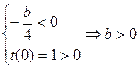 ,
,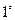 、
、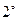 得
得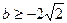 .…………………………………………………………4分
.…………………………………………………………4分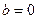 時,
時,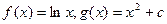 ,設
,設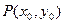 ,
,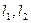 的傾斜角分別為
的傾斜角分別為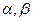 ,則
,則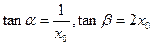 ,由于
,由于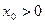 ,則
,則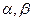 均為銳角,依題,有以下兩種情況:
均為銳角,依題,有以下兩種情況: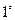
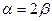 時,
時,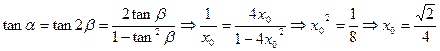 ,
,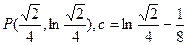 ;
;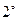
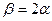 時,
時,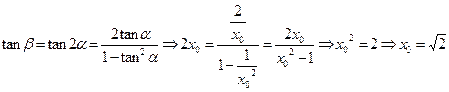 ,
,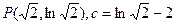 .……………………………………………………9分
.……………………………………………………9分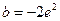 時,令
時,令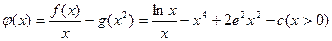
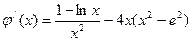 ,
,  時,
時,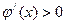 ;
;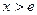 時,
時,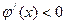
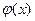 在
在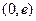 上遞增,在
上遞增,在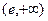 上遞減,∴
上遞減,∴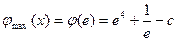 ,
,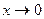 時,
時,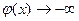 ;
;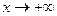 時,
時,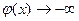
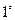
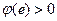 即
即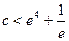 時,函數
時,函數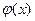 有兩個零點即方程
有兩個零點即方程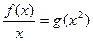 有兩個根;
有兩個根;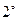
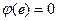 即
即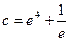 時,函數
時,函數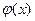 有一個零點即方程
有一個零點即方程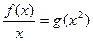 有一個根;
有一個根;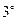
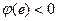 即
即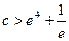 時,函數
時,函數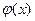 沒有零點即方程
沒有零點即方程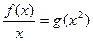 沒有根
沒有根


 天天練口算系列答案
天天練口算系列答案科目:高中數學 來源:不詳 題型:解答題
 的圖象上以N(1,n)為切點的切線的傾斜角為
的圖象上以N(1,n)為切點的切線的傾斜角為
 恒成立?如果存在,請求出最小的正整數k;如果不存在,請說明理由;
恒成立?如果存在,請求出最小的正整數k;如果不存在,請說明理由;
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 ,且函數
,且函數 的圖象關于原點對稱,其圖象在
的圖象關于原點對稱,其圖象在 處的切線方程為
處的切線方程為 (1)求
(1)求 的解析式; (2)是否存在區間
的解析式; (2)是否存在區間 使得函數
使得函數 的定義域和值域均為
的定義域和值域均為 ,且其解析式為f(x)的解析式?若存在,求出這樣的一個區間[m,n];若不存在,則說明理由.
,且其解析式為f(x)的解析式?若存在,求出這樣的一個區間[m,n];若不存在,則說明理由.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
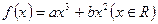 的圖像過點P(-1,2),且在點P處的切線恰好與直線
的圖像過點P(-1,2),且在點P處的切線恰好與直線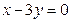 垂直。
垂直。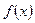 的解析式;
的解析式;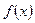 在區間
在區間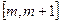 上單調遞增,求實數m的取值范圍。
上單調遞增,求實數m的取值范圍。查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com