
判斷下列對應是不是一一映射
(1)A={1,2,3,4},B={3,5,7,9}對應法則“x乘2加1”
(2)A={1,2,3,4}.B={1,3,5,7,9}對應法則“x乘2加1”
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
|
| a11 | a12 | … | a1m |
| a21 | a22 | … | a2m |
| … | … | … | … |
| an1 | an2 | … | anm |
查看答案和解析>>
科目:高中數學 來源: 題型:
給定項數為![]()
![]() 的數列
的數列![]() ,其中
,其中![]()
![]() .
.
若存在一個正整數![]() ,若數列
,若數列![]() 中存在連續的k項和該數列中另一個連續的k項恰好按次序對應相等,則稱數列
中存在連續的k項和該數列中另一個連續的k項恰好按次序對應相等,則稱數列![]() 是“k階可重復數列”,
是“k階可重復數列”,
例如數列![]()
![]()
因為![]() 與
與![]() 按次序對應相等,所以數列
按次序對應相等,所以數列![]() 是“4階可重復數列”.
是“4階可重復數列”.
(Ⅰ)分別判斷下列數列
①![]() ②
②![]()
是否是“5階可重復數列”?如果是,請寫出重復的這5項;
(Ⅱ)若數為![]() 的數列
的數列![]() 一定是 “3階可重復數列”,則
一定是 “3階可重復數列”,則![]() 的最小值是多少?說明理由;
的最小值是多少?說明理由;
(III)假設數列![]() 不是“5階可重復數列”,若在其最后一項
不是“5階可重復數列”,若在其最后一項![]() 后再添加一項0或1,均可使新數列是“5階可重復數列”,且
后再添加一項0或1,均可使新數列是“5階可重復數列”,且![]() ,求數列
,求數列![]() 的最后一項
的最后一項![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
給定項數為![]()
![]() 的數列
的數列![]() ,其中
,其中![]()
![]() .
.
若存在一個正整數![]() ,若數列
,若數列![]() 中存在連續的k項和該數列中另一個連續的k項恰好按次序對應相等,則稱數列
中存在連續的k項和該數列中另一個連續的k項恰好按次序對應相等,則稱數列![]() 是“k階可重復數列”,
是“k階可重復數列”,
例如數列![]()
![]()
因為![]() 與
與![]() 按次序對應相等,所以數列
按次序對應相等,所以數列![]() 是“4階可重復數列”.
是“4階可重復數列”.
(Ⅰ)分別判斷下列數列
①![]() ②
②![]()
是否是“5階可重復數列”?如果是,請寫出重復的這5項;
(Ⅱ)若數為![]() 的數列
的數列![]() 一定是 “3階可重復數列”,則
一定是 “3階可重復數列”,則![]() 的最小值是多少?說明理由;
的最小值是多少?說明理由;
(III)假設數列![]() 不是“5階可重復數列”,若在其最后一項
不是“5階可重復數列”,若在其最后一項![]() 后再添加一項0或1,均可使新數列是“5階可重復數列”,且
后再添加一項0或1,均可使新數列是“5階可重復數列”,且![]() ,求數列
,求數列![]() 的最后一項
的最后一項![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年北京市西城區高三二模考試理科數學 題型:解答題
((本小題滿分13分)
若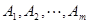 為集合
為集合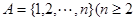 且
且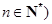 的子集,且滿足兩個條件:
的子集,且滿足兩個條件:
① ;
;
②對任意的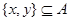 ,至少存在一個
,至少存在一個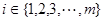 ,使
,使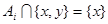 或
或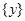 .
.
則稱集合組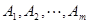 具有性質
具有性質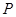 .
.
如圖,作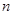 行
行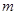 列數表,定義數表中的第
列數表,定義數表中的第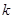 行第
行第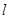 列的數為
列的數為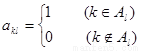 .
.
|
|
|
… |
|
|
|
|
… |
|
|
… |
… |
… |
… |
|
|
|
… |
|
(Ⅰ)當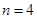 時,判斷下列兩個集合組是否具有性質
時,判斷下列兩個集合組是否具有性質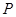 ,如果是請畫出所對應的表格,如果不是請說明理由;
,如果是請畫出所對應的表格,如果不是請說明理由;
集合組1: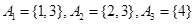 ;
;
集合組2: .
.
(Ⅱ)當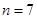 時,若集合組
時,若集合組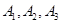 具有性質
具有性質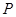 ,請先畫出所對應的
,請先畫出所對應的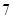 行3列的一個數表,再依此表格分別寫出集合
行3列的一個數表,再依此表格分別寫出集合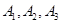 ;
;
(Ⅲ)當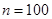 時,集合組
時,集合組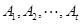 是具有性質
是具有性質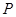 且所含集合個數最小的集合組,求
且所含集合個數最小的集合組,求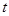 的值及
的值及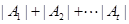 的最小值.(其中
的最小值.(其中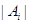 表示集合
表示集合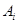 所含元素的個數)
所含元素的個數)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com