
(本題13分)已知函數f (x) = ln(ex + a)(a為常數)是實數集R上的奇函數,函數g (x) =
![]() f (x) + sinx是區間[1,1]上的減函數.
f (x) + sinx是區間[1,1]上的減函數.
(1)求a的值;
(2)若g (x)≤t2 +![]() t + 1在x∈[1,1]上恒成立,求t的取值范圍;
t + 1在x∈[1,1]上恒成立,求t的取值范圍;
(3)討論關于x的方程![]() 的根的個數.
的根的個數.
解析:(1)由于f (x) 是R上的奇函數,f (0) = 0,故a = 0.……………………3分
(2)∵g (x)在[1,1]上單調遞減,∴![]() 時
時![]() 恒成立
恒成立
![]() ,
,![]()
∴只要![]()
∴(t + 1)![]() + t2 + sin1 + 1≥0(其中
+ t2 + sin1 + 1≥0(其中![]() ≤1)恒成立.……………………5分
≤1)恒成立.……………………5分
令![]()
則![]()
∴t≤1.………………………………………………………………………………8分
(3)由(1)知![]() .∴方程為
.∴方程為![]()
令f1(x) =![]() ,f2(x) = x2 2ex + m,
,f2(x) = x2 2ex + m,
∵![]()
當x∈(0,e)時,![]() ,∴
,∴![]() 在(0,e]上為增函數;
在(0,e]上為增函數;
當x∈(e,+∞)時,![]() ,∴
,∴![]() 在(e,+∞)上為減函數;
在(e,+∞)上為減函數;
當x = e時![]() .
.
而![]()
∴當![]() 時,即
時,即![]() 時方程無解.
時方程無解.
當![]() 時,即
時,即![]() 時方程有一解.
時方程有一解.
當![]() 時,即
時,即![]() 時方程有二解.………………………………………13分
時方程有二解.………………………………………13分


科目:高中數學 來源:2011屆陜西省師大附中、西工大附中高三第七次聯考理數 題型:解答題
(本題13分)
已知函數 .
.
(1)當 時,求
時,求 的單調區間;
的單調區間;
(2)若 在
在 單調增加,在
單調增加,在 單調減少,證明:
單調減少,證明: <6.
<6.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年浙江省高一上學期期中考試數學試卷(解析版) 題型:解答題
(本題13分)已知函數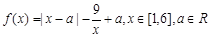 。
。
(Ⅰ)若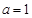 ,試判斷并證明
,試判斷并證明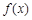 的單調性;
的單調性;
(Ⅱ)若函數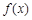 在
在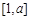 上單調,且存在
上單調,且存在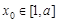 使
使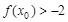 成立,求
成立,求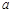 的取值范圍;
的取值范圍;
(Ⅲ)當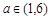 時,求函數
時,求函數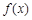 的最大值的表達式
的最大值的表達式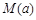 。
。
查看答案和解析>>
科目:高中數學 來源:2012-2013學年安徽省無為縣四高三考文科數學試卷(解析版) 題型:解答題
(本題滿分13分)已知函數f(x)=cos(-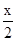 )+cos(
)+cos(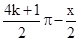 ),k∈Z,x∈R.
),k∈Z,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在[0,π)上的減區間;
(3)若f(α)=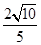 ,α∈(0,
,α∈(0,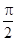 ),求tan(2α+
),求tan(2α+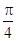 )的值.
)的值.
查看答案和解析>>
科目:高中數學 來源:2010年福建省四地六校聯考高一第三次月考數學卷 題型:解答題
(本題13分)
已知函數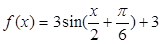 ,
,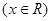

(1)用五點法畫出它在一個周期內的閉區間上的圖象;
(2)說明此函數圖象可由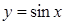 ,
,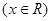 的圖象經怎樣的變換得到.
的圖象經怎樣的變換得到.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com