
已知函數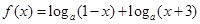 ,其中
,其中 ,記函數
,記函數 的定義域為D.
的定義域為D.
(1)求函數 的定義域D;
的定義域D;
(2)若函數 的最小值為
的最小值為 ,求
,求 的值;
的值;
(3)若對于D內的任意實數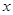 ,不等式
,不等式 <
<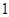 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.
(1)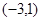
(2) 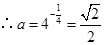
(3) (-∞, )∪[
)∪[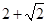 ,+∞)
,+∞)
解析試題分析:解:(1)要使函數有意義:則有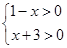 ,解得
,解得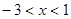
∴ 函數的定義域D為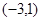 2分
2分
(2)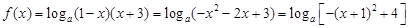
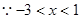
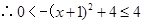
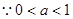 ,
,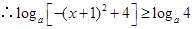 ,即
,即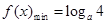 , 5分
, 5分
由 ,得
,得 ,
,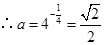 . 7分
. 7分
(注: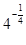 不化簡為
不化簡為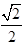 扣1分)
扣1分)
(3)由題知-x2+2mx-m2+2m<1在x∈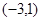 上恒成立,
上恒成立,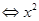 -2mx+m2-2m+1>0在x∈
-2mx+m2-2m+1>0在x∈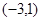 上恒成立, 8分
上恒成立, 8分
令g(x)=x2-2mx+m2-2m+1,x∈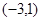 ,
,
配方得g(x)=(x-m)2-2m+1,其對稱軸為x=m,
當m≤-3時, g(x)在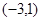 為增函數,
為增函數,
∴g(-3)= (-3-m)2-2m+1= m2+4m +10≥0,
而m2+4m +10≥0對任意實數m恒成立,∴m≤-3. 10分
②當-3<m<1時,函數g(x)在(-3,-1)為減函數,在(-1, 1)為增函數,
∴g(m)=-2m+1>0,解得m<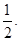 ∴-3<m<
∴-3<m< 12分
12分
③當m≥1時,函數g(x)在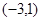 為減函數,∴g(1)= (1-m)2-2m+1= m2-4m +2≥0,
為減函數,∴g(1)= (1-m)2-2m+1= m2-4m +2≥0,
解得m≥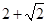 或m≤
或m≤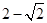 , ∴-3<m<
, ∴-3<m< 14分
14分
綜上可得,實數m的取值范圍是 (-∞, )∪[
)∪[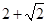 ,+∞) 16分
,+∞) 16分
考點:函數的概念和值域,二次函數的最值
點評:解決的關鍵是利用函數的概念以及分離參數的思想來借助于二次函數的最值得到參數的范圍。屬于基礎題。


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
定義在R上的函數f(x)是最小正周期為2的奇函數, 且當x∈(0, 1)時, f (x)=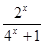 .
.
(1)求f (x)在[-1, 1]上的解析式;
(2)證明f (x)在(—1, 0)上時減函數;
(3)當λ取何值時, 不等式f (x)>λ在R上有解?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
)設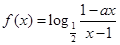 為奇函數,
為奇函數, 為常數.
為常數.
(1)求 的值;
的值;
(2)判斷 在區(qū)間(1,+∞)內的單調性,并證明你的判斷正確;
在區(qū)間(1,+∞)內的單調性,并證明你的判斷正確;
(3)若對于區(qū)間 [3,4]上的每一個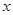 的值,不等式
的值,不等式 >
>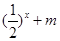 恒成立,求實數
恒成立,求實數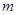 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,已知正比例函數y=2x的圖像l1與反比例函數y= 的圖像相交于點A(a,2),將直線l1向上平移3個單位得到的直線l2與雙曲線相交于B、C兩點(點B在第一象限),與y軸交于點D.
的圖像相交于點A(a,2),將直線l1向上平移3個單位得到的直線l2與雙曲線相交于B、C兩點(點B在第一象限),與y軸交于點D.
(1)求反比例函數的解析式;
(2)求△DOB的面積.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com