
對于定義域為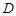 的函數
的函數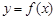 ,若有常數M,使得對任意的
,若有常數M,使得對任意的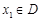 ,存在唯一的
,存在唯一的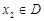 滿足等式
滿足等式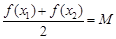 ,則稱M為函數
,則稱M為函數 f (x)的“均值”.
f (x)的“均值”.
(1)判斷1是否為函數 ≤
≤ ≤
≤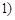 的“均值”,請說明理由;
的“均值”,請說明理由;
(2)若函數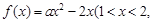
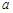 為常數)存在“均值”,求實數a的取值范圍;
為常數)存在“均值”,求實數a的取值范圍;
(3)若函數 是單調函數,且其值域為區間I.試探究函數
是單調函數,且其值域為區間I.試探究函數 的“均值”情況(是否存在、個數、大小等)與區間I之間的關系,寫出你的結論(不必證明).
的“均值”情況(是否存在、個數、大小等)與區間I之間的關系,寫出你的結論(不必證明).
說明:對于(3),將根據結論的完整性與一般性程度給予不同的評分
解:(1)對任意的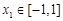 ,有
,有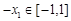 ,
,
當且僅當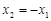 時,有
時,有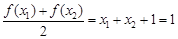 ,
,
故存在唯一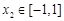 ,滿足
,滿足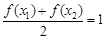 ,
……………………2分
,
……………………2分
所以1是函數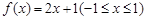 的“均值”.
……………………4分
的“均值”.
……………………4分
(另法:對任意的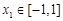 ,有
,有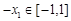 ,令
,令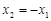 ,
,
則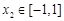 ,且
,且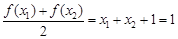 ,
[來源:]
,
[來源:]
若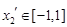 ,且
,且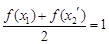 ,則有
,則有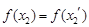 ,可得
,可得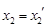 ,
,
故存在唯一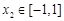 ,滿足
,滿足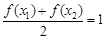 ,
……………………2分
,
……………………2分
所以1是函數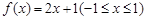 的“均值”.
……………………4分)
的“均值”.
……………………4分)
(2)當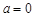 時,
時, 存在“均值”,且“均值”為
存在“均值”,且“均值”為 ;…………5分
;…………5分
當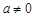 時,由
時,由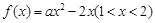 存在均值,可知對任意的
存在均值,可知對任意的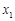 ,
,
都有唯一的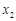 與之對應,從而有
與之對應,從而有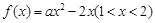 單調,
單調,
故有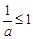 或
或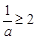 ,解得
,解得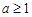 或
或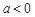 或
或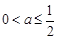 ,
……………………9分
,
……………………9分
綜上,a的取值范圍是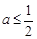 或
或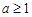 . ……………………10分
. ……………………10分
(另法:分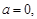
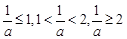 四種情形進行討論)
四種情形進行討論)
(3)①當I
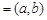 或
或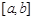 時,函數
時,函數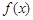 存在唯一的“均值”.
存在唯一的“均值”.
這時函數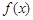 的“均值”為
的“均值”為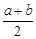 ;
…………………12分
;
…………………12分
②當I為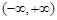 時,函數
時,函數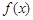 存在無數多個“均值”.
存在無數多個“均值”.
這時任意實數均為函數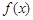 的“均值”; ……………………14分
的“均值”; ……………………14分
③當I
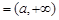 或
或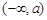 或
或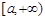 或
或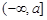 或
或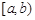 或
或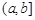 時,
時,
函數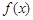 不存在“均值”. ……………………16分
不存在“均值”. ……………………16分
[評分說明:若三種情況討論完整且正確,但未用等價形式進行敘述,至多得6分;若三種情況討論不完整,且未用等價形式敘述,至多得5分]
①當且僅當I形如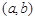 、
、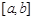 其中之一時,函數
其中之一時,函數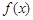 存在唯一的“均值”.
存在唯一的“均值”.
這時函數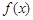 的“均值”為
的“均值”為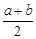 ;
……………………13分
;
……………………13分
②當且僅當I為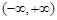 時,函數
時,函數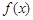 存在無數多個“均值”.
存在無數多個“均值”.
這時任意實數均為函數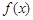 的“均值”; ……………………16分
的“均值”; ……………………16分
③當且僅當I形如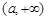 、
、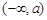 、
、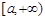 、
、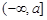 、
、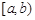 、
、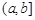 其中之一時,函數
其中之一時,函數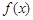 不存在“均值”. ……………………18分
不存在“均值”. ……………………18分
(另法:①當且僅當I為開區間或閉區間時,函數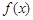 存在唯一的“均值”.這時函數
存在唯一的“均值”.這時函數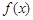 的均值為區間I兩端點的算術平均數;
……………………13分
的均值為區間I兩端點的算術平均數;
……………………13分
②當且僅當I為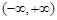 時,函數
時,函數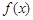 存在無數多個“均值”.這時任意實數均為函數
存在無數多個“均值”.這時任意實數均為函數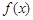 的“均值”;
……………………16分
的“均值”;
……………………16分
③當且僅當I為除去開區間、閉區間與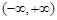 之外的其它區間時,函數
之外的其它區間時,函數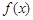 不存在“均值”.
……………………18分)
不存在“均值”.
……………………18分)
[評分說明:在情形①與②中,等價關系敘述正確但未正確求出函數“均值”,各扣1分]
【解析】略


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
對于定義域為![]() 的函數
的函數![]() ,若同時滿足:①
,若同時滿足:①![]() 在
在![]() 內單調遞增或單調遞減;②存在區間
內單調遞增或單調遞減;②存在區間![]()
![]() ,使
,使![]() 在
在![]() 上的值域為
上的值域為![]() ;那么把函數
;那么把函數![]() (
(![]() )叫做閉函數.
)叫做閉函數.
(1) 求閉函數![]() 符合條件②的區間
符合條件②的區間![]() ;
;
(2) 若![]() 是閉函數,求實數
是閉函數,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本題滿分14分)定義:對于函數![]() ,
,![]() .若
.若![]() 對定義域內的
對定義域內的![]() 恒成立,則稱函數
恒成立,則稱函數![]() 為
為![]() 函數.(1)請舉出一個定義域為
函數.(1)請舉出一個定義域為![]() 的
的![]() 函數,并說明理由;(2)對于定義域為
函數,并說明理由;(2)對于定義域為![]() 的
的![]() 函數
函數![]() ,求證:對于定義域內的任意正數
,求證:對于定義域內的任意正數![]() ,均有
,均有![]()
![]() ;
;
(3)對于值域![]() 的
的![]() 函數
函數![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源:2011屆上海市盧灣區高考模擬考試數學試卷(理科) 題型:解答題
對于定義域為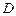 的函數
的函數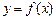 ,若有常數M,使得對任意的
,若有常數M,使得對任意的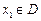 ,存在唯一的
,存在唯一的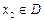 滿足等式
滿足等式 ,則稱M為函數
,則稱M為函數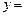 f (x)的“均值”.
f (x)的“均值”.
(1)判斷1是否為函數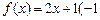 ≤
≤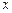 ≤
≤ 的“均值”,請說明理由;
的“均值”,請說明理由;
(2)若函數
 為常數)存在“均值”,求實數a的取值范圍;
為常數)存在“均值”,求實數a的取值范圍;
(3)若函數 是單調函數,且其值域為區間I.試探究函數
是單調函數,且其值域為區間I.試探究函數 的“均值”情況(是否存在、個數、大小等)與區間I之間的關系,寫出你的結論(不必證明).
的“均值”情況(是否存在、個數、大小等)與區間I之間的關系,寫出你的結論(不必證明).
說明:對于(3),將根據結論的完整性與一般性程度給予不同的評分
查看答案和解析>>
科目:高中數學 來源:2015屆廣東省高一下學期期末考試數學試卷(解析版) 題型:填空題
對于定義域為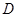 的函數
的函數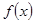 ,若存在區間
,若存在區間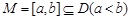 ,使得
,使得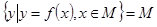 則稱區間M為函數
則稱區間M為函數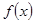 的“等值區間”.給出下列三個函數:
的“等值區間”.給出下列三個函數:
① ; ②
; ②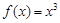 ; ③
; ③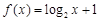
則存在“等值區間”的函數的個數是___________.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年上海市崇明縣高三第一學期期末考試數學 題型:填空題
定義:對于定義域為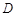 的函數
的函數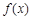 ,如果存在
,如果存在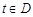 ,使得
,使得 成立,稱函數
成立,稱函數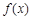 在
在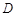 上是“
上是“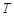 ”函數。已知下列函數:①
”函數。已知下列函數:①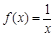 ; ②
; ②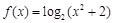 ;③
;③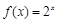 (
(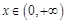 ); ④
); ④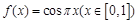 ,其中屬于“
,其中屬于“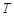 ”函數的序號是 .(寫出所有滿足要求的函數的序號)
”函數的序號是 .(寫出所有滿足要求的函數的序號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com