
(本小題滿分16分)
已知函數 ,
,
(1)若 在
在 上的最大值為
上的最大值為 ,求實數
,求實數 的值;
的值;
(2)若對任意 ,都有
,都有 恒成立,求實數
恒成立,求實數 的取值范圍;
的取值范圍;
(3)在(1)的條件下,設 ,對任意給定的正實數
,對任意給定的正實數 ,曲線
,曲線 上是否存在兩點
上是否存在兩點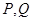 ,使得
,使得 是以
是以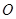 (
(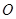 為坐標原點)為直角頂點的直角三角形,且此三角形斜邊中點在
為坐標原點)為直角頂點的直角三角形,且此三角形斜邊中點在 軸上?請說明理由。
軸上?請說明理由。
(1)b=0;(2) ;(3)對任意給定的正實數
;(3)對任意給定的正實數 ,曲線
,曲線 上總存在兩點
上總存在兩點 ,使得
,使得 是以
是以 (
( 為坐標原點)為直角頂點的直角三角形,且此三角形斜邊中點在
為坐標原點)為直角頂點的直角三角形,且此三角形斜邊中點在 軸上.
軸上.
【解析】
試題分析:(1)由 ,得
,得 ,
,
令 ,得
,得 或
或 .
.
列表如下:
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
極小值 |
|
極大值 |
|
由 ,
, ,
, ,
,
即最大值為 ,
, .
………………………………5分
.
………………………………5分
(2)由 ,得
,得 .
.
 ,且等號不能同時取,
,且等號不能同時取, ,
,
 恒成立,即
恒成立,即 .
………………………………7分
.
………………………………7分
令 ,求導得,
,求導得, ,
,
當 時,
時, ,從而
,從而 ,
,
 在
在 上為增函數,
上為增函數, ,
, . …………………10分
. …………………10分
(3)由條件, ,
,
假設曲線 上存在兩點
上存在兩點 滿足題意,則
滿足題意,則 只能在
只能在 軸兩側,
軸兩側,
不妨設 ,則
,則 ,且
,且 .
.
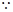
 是以
是以 (
( 為坐標原點)為直角頂點的直角三角形,
為坐標原點)為直角頂點的直角三角形,
 ,
,
 ,
,
是否存在 等價于方程
等價于方程 在
在 且
且 時是否有解.
…………………12分
時是否有解.
…………………12分
①若 時,方程
時,方程 為
為 ,化簡得
,化簡得 ,
,
此方程無解;
②若 時,
時, 方程為
方程為 ,即
,即 ,
,
設 ,則
,則 ,
,
顯然,當 時,
時, ,即
,即 在
在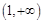 上為增函數,
上為增函數,
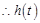 的值域為
的值域為 ,即
,即 ,
,
 當
當 時,方程
時,方程 總有解.
總有解.
 對任意給定的正實數
對任意給定的正實數 ,曲線
,曲線 上總存在兩點
上總存在兩點 ,使得
,使得 是以
是以 (
( 為坐標原點)為直角頂點的直角三角形,且此三角形斜邊中點在
為坐標原點)為直角頂點的直角三角形,且此三角形斜邊中點在 軸上.………………16分
軸上.………………16分
考點:本題考查了導數在函數中的運用
點評:解此類題時要注意對數式對函數定義域的隱蔽,這類問題重點考查函數單調性、導數運算、不等式方程的求解等基本知識,注重數學思想(分類與整合、數與形的結合)方法(分析法、綜合法、反證法)的運用.把數學運算的“力量”與數學思維的“技巧”完美結合.


科目:高中數學 來源: 題型:
(2010江蘇卷)18、(本小題滿分16分)
 在平面直角坐標系
在平面直角坐標系![]() 中,如圖,已知橢圓
中,如圖,已知橢圓![]() 的左、右頂點為A、B,右焦點為F。設過點T(
的左、右頂點為A、B,右焦點為F。設過點T(![]() )的直線TA、TB與橢圓分別交于點M
)的直線TA、TB與橢圓分別交于點M![]() 、
、![]() ,其中m>0,
,其中m>0,![]() 。
。
(1)設動點P滿足![]() ,求點P的軌跡;
,求點P的軌跡;
(2)設![]() ,求點T的坐標;
,求點T的坐標;
(3)設![]() ,求證:直線MN必過x軸上的一定點(其坐標與m無關)。
,求證:直線MN必過x軸上的一定點(其坐標與m無關)。
查看答案和解析>>
科目:高中數學 來源:2010年泰州中學高一下學期期末測試數學 題型:解答題
(本小題滿分16分)
函數 ,
, (
( ),
),
A=
(Ⅰ)求集合A;
(Ⅱ)如果 ,對任意
,對任意 時,
時, 恒成立,求實數
恒成立,求實數 的范圍;
的范圍;
(Ⅲ)如果 ,當“
,當“ 對任意
對任意 恒成立”與“
恒成立”與“ 在
在 內必有解”同時成立時,求
內必有解”同時成立時,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源:2014屆江蘇大豐新豐中學高二上期中考試文數學試卷(解析版) 題型:解答題
(本小題滿分16分) 本題請注意換算單位
某開發商用9000萬元在市區購買一塊土地建一幢寫字樓,規劃要求寫字樓每層建筑面積為2000平方米。已知該寫字樓第一層的建筑費用為每平方米4000元,從第二層開始,每一層的建筑費用比其下面一層每平方米增加100元。
(1)若該寫字樓共x層,總開發費用為y萬元,求函數y=f(x)的表達式;
(總開發費用=總建筑費用+購地費用)
(2)要使整幢寫字樓每平方米開發費用最低,該寫字樓應建為多少層?
查看答案和解析>>
科目:高中數學 來源:2013屆安徽省蚌埠市高二下學期期中聯考文科數學試卷(解析版) 題型:解答題
(本小題滿分16分)設命題 :方程
:方程 無實數根;
命題
無實數根;
命題 :函數
:函數
 的值域是
的值域是 .如果命題
.如果命題 為真命題,
為真命題, 為假命題,求實數
為假命題,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010年江蘇省高一第三階段檢測數學卷 題型:解答題
(本小題滿分16分)
已知函數f(x)= 為偶函數,且函數y=f(x)圖象的兩相鄰對稱軸間的距離為
為偶函數,且函數y=f(x)圖象的兩相鄰對稱軸間的距離為
(Ⅰ)求f( )的值;
)的值;
(Ⅱ)將函數y=f(x)的圖象向右平移 個單位后,再將得到的圖象上各點的橫坐標延長到原來的4倍,縱坐標不變,得到函數y=g(x)的圖象,求g(x)的單調遞減區間.
個單位后,再將得到的圖象上各點的橫坐標延長到原來的4倍,縱坐標不變,得到函數y=g(x)的圖象,求g(x)的單調遞減區間.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com