中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

在某種產品表面進行腐蝕性刻線實驗，得到腐蝕深度y與腐蝕時間x之間相應的一組觀察值，如下表：

x/s
5
10
15
20
30
40
50
60
70
90
120
y/μm
6
10
10
13
16
17
19
23
25
29
46
用散點圖及相關系數兩種方法判斷x與y的相關性．

作出如圖所示的散點圖．

腐蝕深度y與腐蝕時間x之間有很強的線性相關關系

解析解:(1)作出如圖所示的散點圖．

從散點圖可看出腐蝕深度y(μm)與腐蝕時間x(s)之間存在著較強的線性相關關系．
(2)相關系數r＝
＝≈0.98，
顯然|r|＞0.75.所以，腐蝕深度y與腐蝕時間x之間有很強的線性相關關系．

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：解答題

某普通高中共有教師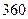人，分為三個批次參加研修培訓，在三個批次中男、女教師人數如下表所示：

 
第一批次
第二批次
第三批次
女教師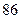



男教師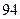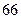



 
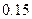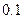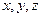已知在全體教師中隨機抽取1名，抽到第二、三批次中女教師的概率分別是、．
（1）求的值；
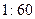（2）為了調查研修效果，現從三個批次中按的比例抽取教師進行問卷調查，三個批次被選取的人數分別是多少？
（3）若從（2）中選取的教師中隨機選出兩名教師進行訪談，求參加訪談的兩名教師“分別來自兩個批次”的概率．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

為預防X病毒爆發,某生物技術公司研制出一種X病毒疫苗,為測試該疫苗的有效性(若疫苗有效的概率小于90%,則認為測試沒有通過),公司選定2000個樣本分成三組,測試結果如下表:

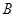分組
組
組
組
疫苗有效
673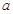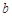


疫苗無效
77
90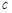

 
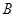已知在全體樣本中隨機抽取1個，抽到組疫苗有效的概率是0．33．
（1）現用分層抽樣的方法在全體樣本中抽取360個測試結果，應在組抽取樣本多少個?
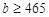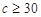（2）已知，，求通過測試的概率．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

某學校為了選拔學生參加“XX市中學生知識競賽”，先在本校進行選拔測試（滿分150分），若該校有100名學生參加選拔測試，并根據選拔測試成績作出如圖所示的頻率分布直方圖．
（1）根據頻率分布直方圖，估算這100名學生參加選拔測試的平均成績；
（2）該校推薦選拔測試成績在110以上的學生代表學校參加市知識競賽，為了了解情況，在該校推薦參加市知識競賽的學生中隨機抽取2人，求選取的兩人的選拔成績在頻率分布直方圖中處于不同組的概率．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

某種水果的單個質量在500g以上視為特等品.隨機抽取1000個該水果，結果有50個特等品.將這50個水果的質量數據分組，得到下邊的頻率分布表.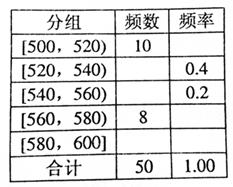

（1）估計該水果的質量不少于560g的概率；
（2）若在某批水果的檢測中，發現有15個特等品，據此估計該批水果中沒有達到特等品的個數.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

某企業有兩個分廠生產某種零件，按規定內徑尺寸(單位：mm)的值落在[29.94,30.06)的零件為優質品．從兩個分廠生產的零件中各抽出了500件，量其內徑尺寸，得結果如下表：
甲廠：

分組
 		[29.86，29.90)
 		[29.90，29.94)
 		[29.94，29.98)
 		[29.9830.02)，
 		[30.02，30.06)
 		[30.06，30.10)
 		[30.10，30.14)
 
頻數
 		12
 		63
 		86
 		182
 		92
 		61
 		4
 
乙廠：
分組
 		[29.86，29.90)
 		[29.90，29.94)
 		[29.94，29.98)
 		[29.9830.02)，
 		[30.02，30.06)
 		[30.06，30.10)
 		[30.10，30.14)
 
頻數
 		29
 		71
 		85
 		159
 		76
 		62
 		18
 
 
(1)試分別估計兩個分廠生產的零件的優質品率；
(2)由以上統計數據填下面2×2列聯表，并問是否有99%的把握認為“兩個分廠生產的零件的質量有差異”？
 
 		甲廠
 		乙廠
 		合計
 
優質品
 		 
 		 
 		 
 
非優質品
 		 
 		 
 		 
 
合　計
 		 
 		 
 		 
 
附：
P(χ2≥x0)
 		0.05
 		0.01
 
x0
 		3.841
 		6.635
 
 

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

某市為“市中學生知識競賽”進行選拔性測試，且規定：成績大于或等于90分的有參賽資格，90分以下（不包括90分）的被淘汰.若有500人參加測試，學生成績的頻率分布直方圖如圖.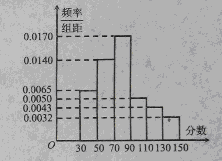

(1)求獲得參賽資格的人數；
(2)根據頻率直方圖，估算這500名學生測試的平均成績；
(3)若知識競賽分初賽和復賽，在初賽中每人最多有5次選題答題的機會，累計答對3題或答錯3題即終止，答對3題者方可參加復賽.已知參賽者甲答對每一個問題的概率都相同，并且相互之間沒有影響.已知他連續兩次答錯的概率為，求甲在初賽中答題個數的分布列及數學期望.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

某地區有小學21所，中學14所，大學7所，現采用分層抽樣的方法從這些學校中抽取6所學校對學生進行視力調查．
(1)求應從小學、中學、大學中分別抽取的學校數目；
(2)若從抽取的6所學校中隨機抽取2所學校做進一步數據分析，
①列出所有可能的抽取結果；
②求抽取的2所學校均為小學的概率．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

衡水某中學對高二甲、乙兩個同類班級進行“加強‘語文閱讀理解’訓練對提高‘數學應用題’得分率作用”的試驗,其中甲班為試驗班(加強語文閱讀理解訓練),乙班為對比班(常規教學,無額外訓練),在試驗前的測試中,甲、乙兩班學生在數學應用題上的得分率基本一致,試驗結束后,統計幾次數學應用題測試的平均成績(均取整數)如下表所示:

 
60分
以下
61～
70分
71～
80分
81～
90分
91～
100分
甲班
(人數)
3
6
11
18
12
乙班
(人數)
4
8
13
15
10
現規定平均成績在80分以上(不含80分)的為優秀.
(1)試分別估計兩個班級的優秀率.
(2)由以上統計數據填寫下面2×2列聯表,并判斷“加強‘語文閱讀理解’訓練對提高‘數學應用題’得分率”是否有幫助?
 
優秀人數
非優秀人數
總計
甲班
 
 
 
乙班
 
 
 
總計
 
 
 
參考公式及數據:K2=,

查看答案和解析>>

同步練習冊答案