已知函數
（1）求函數的最小正周期；
（2）當
時，求函數
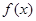的值域；
（3）先將函數
的圖象向左平移
個單位得到函數
的圖象，再將的圖象橫坐標擴大到原來的2倍縱坐標不變，得到函數
的圖象，求證：直線
與的圖象相切于
（1）
；（2）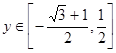
；（3）詳見解析
解析試題分析：（1）本小題首先需要把函數化簡可得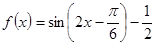
，然后根據三角函數周期公式
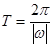可求得目標函數最小正周期
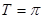；（2）首先根據
的取值范圍求得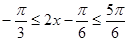
，結合正弦函數的圖像可求得
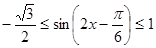，從而可求得函數的值域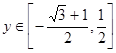；（3）首先根據函數圖像的各種平移變化，可求得
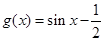，然后利用導數的幾何意義求得曲線的切線方程，從而可證明結論.
試題解析：(1)由已知可得：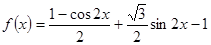
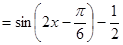
故函數的最小正周期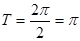
（2）因為，所以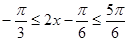
所以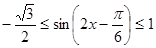
所以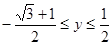
即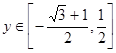
（3）將函數的圖象向左平移個單位得到函數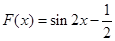
，
再將的圖象橫坐標擴大到原來的2倍縱坐標不變，
得到函數。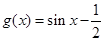
因為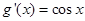
，
所以切線的斜率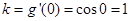
，
而切點為
所以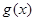
的切線方程為
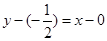，即
所以直線與的圖象相切于
考點：1.三角函數的圖像與性質；2.平移變換；3.導數的幾何意義.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：解答題
已知真命題:“函數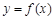
的圖像關于點
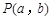成中心對稱圖形”的充要條件為“函數
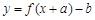是奇函數”.
（Ⅰ）將函數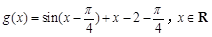
的圖像向左平移
個單位，再向上平移2個單位，求此時圖像對應的函數解析式，并利用題設中的真命題求函數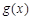
圖像對稱中心的坐標；
（Ⅱ）求函數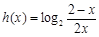
圖像對稱中心的坐標；
（Ⅲ）已知命題：“函數 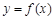的圖像關于某直線成軸對稱圖像”的充要條件為“存在實數
和
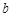，使得函數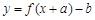 是偶函數”.判斷該命題的真假，如果是真命題，請給予證明；如果是假命題，請說明理由，并類比題設的真命題對它進行修改，使之成為真命題(不必證明).
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知函數
，且當
時，
的最小值為2.
（1）求
的值，并求的單調增區間；
（2）將函數
的圖象上各點的縱坐標保持不變，橫坐標縮短到原來的
，再把所得圖象向右平移
個單位，得到函數
，求方程
在區間
上的所有根之和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
函數
滿足
.
的單調遞減區間；
的內角
所對的邊分別為
，且
，求
的取值范圍.
，
．
，求
的值；
，
，求
的值．
，設∠CAB＝α，
，其中
，求
的值.
．
的取值范圍．
中，角
的對邊分別為
.
，求
的值；
，求
的值．
，
，其中
．
；（2）求
的值．