
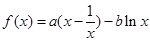 (
(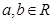 ),
),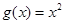 .
.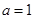 ,曲線
,曲線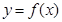 在點
在點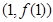 處的切線與
處的切線與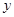 軸垂直,求
軸垂直,求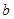 的值;
的值;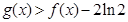 ;
;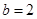 ,試探究函數
,試探究函數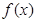 與
與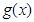 的圖象在其公共點處是否存在公切線,若存在,研究
的圖象在其公共點處是否存在公切線,若存在,研究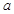 值的個數;若不存在,請說明理由.
值的個數;若不存在,請說明理由.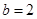 (Ⅱ)見解析(Ⅲ)當
(Ⅱ)見解析(Ⅲ)當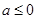 時,函數
時,函數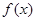 與
與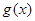 的圖象在其公共點處不存在公切線;當
的圖象在其公共點處不存在公切線;當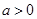 時,函數
時,函數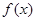 與
與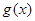 的圖象在其公共點處存在公切線,且符合題意的
的圖象在其公共點處存在公切線,且符合題意的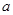 值有且僅有兩個
值有且僅有兩個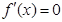 建立關于b的方程,求出b值.
建立關于b的方程,求出b值.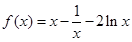 ,定義域為
,定義域為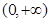 ,要證
,要證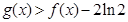 ,
,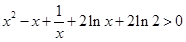 ,然后構造函數
,然后構造函數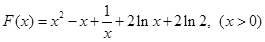 ,
, 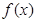 與
與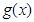 的圖象在其公共點
的圖象在其公共點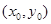 處存在公切線,則滿足
處存在公切線,則滿足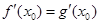 ,所以
,所以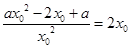 ,即
,即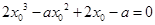 ,從而求出
,從而求出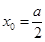 ,
,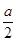 是否大于零來確定假設是否成立.
是否大于零來確定假設是否成立.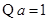 ,
,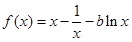 ,
,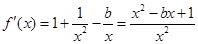 , --------------------------2分
, --------------------------2分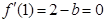 ,∴
,∴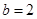 . --------------------------3分
. --------------------------3分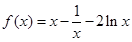 ,定義域為
,定義域為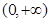 ,
,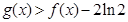 ,只須證
,只須證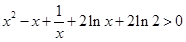 ,
,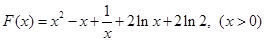 , -------------------4分
, -------------------4分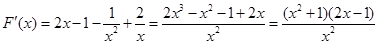 ,
,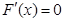 ,得
,得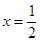 , ---------------------------6分
, ---------------------------6分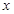 | 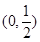 | 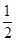 | 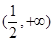 |
 | 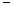 | 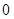 | 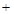 |
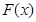 | 遞減 | 極小 | 遞增 |
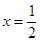 時,
時,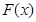 取極小值也是最小值,且
取極小值也是最小值,且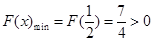 ,
,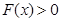 ,∴
,∴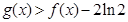 . --------------------8分
. --------------------8分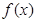 與
與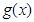 的圖象在其公共點
的圖象在其公共點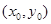 處存在公切線,
處存在公切線,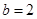 ,∴
,∴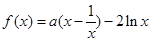 ,
,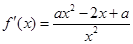 ,
,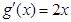 ,由
,由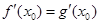 得,
得,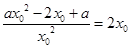 ,
,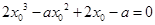 ,∴
,∴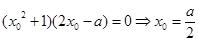 ,--------------9分
,--------------9分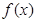 的定義域為
的定義域為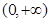 ,
,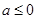 時,
時,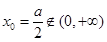 ,∴函數
,∴函數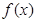 與
與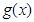 的圖象在其公共點處不存在公切線;---10分
的圖象在其公共點處不存在公切線;---10分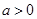 時,令
時,令 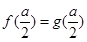 ,∵
,∵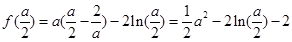 ,
,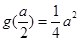 ,
,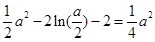 ,即
,即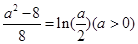 , ----------------11分
, ----------------11分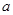 值的個數:
值的個數: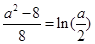 得
得 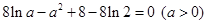 ,
, 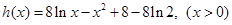 ,
,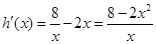 ,
,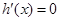 得
得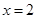 ,當
,當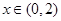 時,
時,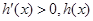 遞增;
遞增;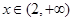 時,
時,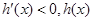 遞減;
遞減;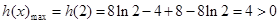 ,又
,又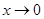 時,
時,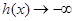 ,
,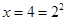 時,
時,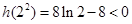 ,
,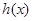 的圖象與
的圖象與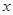 軸有且僅有兩個交點,即符合題意的
軸有且僅有兩個交點,即符合題意的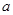 值有且僅有兩個.
值有且僅有兩個.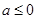 時,函數
時,函數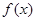 與
與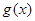 的圖象在其公共點處不存在公切線;
的圖象在其公共點處不存在公切線;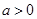 時,函數
時,函數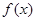 與
與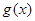 的圖象在其公共點處存在公切線,
的圖象在其公共點處存在公切線,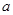 值有且僅有兩個.-------------------------------14分
值有且僅有兩個.-------------------------------14分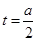 ,則
,則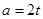 ,且
,且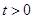 ,方程
,方程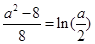 化為
化為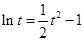 ,
,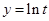 和
和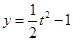 的圖象,因為
的圖象,因為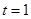 時,
時,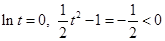 ,
,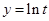 和
和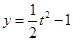 圖象有且只有兩個公共點(且均符合
圖象有且只有兩個公共點(且均符合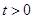 ),
),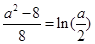 有且只有兩個解.
有且只有兩個解.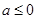 時,函數
時,函數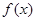 與
與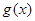 的圖象在其公共點處不存在公切線;
的圖象在其公共點處不存在公切線;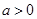 時,函數
時,函數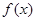 與
與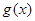 的圖象在其公共點處存在公切線,
的圖象在其公共點處存在公切線,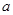 值有且僅有兩個.--------------------------------14分
值有且僅有兩個.--------------------------------14分

 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com