
(09年海淀區期末文)(14分)
直三棱柱A1B1C1―ABC中,![]()
(I)求證:BC1//平面A1CD;
(II)求二面角A―A1C―D的大小。

解析:(I)證明:連結AC1,設![]() 連結DE,…………1分
連結DE,…………1分
![]() A1B1C1―ABC是直三棱柱,且
A1B1C1―ABC是直三棱柱,且![]()
![]() AA1CC1是正方形,E是AC1的中點,
AA1CC1是正方形,E是AC1的中點,
又D為AB中點,
![]() ED//BC1…………3分
ED//BC1…………3分
又![]()
![]() BC1//平面A1CD…………5分
BC1//平面A1CD…………5分
(II)法一:設H是AC中點,F是EC中點,連接DH,HF,FD…………6分
|
![]() D為AB中點,
D為AB中點,
![]() DH//BC,同理可證HF//AE,
DH//BC,同理可證HF//AE,
又![]()
又側棱![]()
![]()
![]() …………8分
…………8分
由(I)得AA1C1C是正方形,則![]()
![]()
![]() 在平面AA1C1C上的射影,
在平面AA1C1C上的射影,
![]()
![]() 是二面角A―A1C―D的平面角…………10分
是二面角A―A1C―D的平面角…………10分
又![]() ……12分
……12分
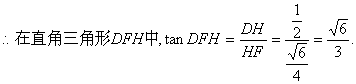 …………13分
…………13分
![]() …………14分
…………14分
法二:在直三棱柱A1B1C1―ABC中,
![]() 分別以CA,CB,CC1所在的直線為
分別以CA,CB,CC1所在的直線為![]() 建立空間直角坐標系,
建立空間直角坐標系,
![]()
則![]() ……7分
……7分
|
設平面A1DC的法向量為![]() 則
則
 …………8分
…………8分
![]()
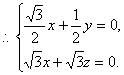
則 …………9分
…………9分
取![]() ……10分
……10分
![]() 為平面CAA1C1的一個法向量…………11分
為平面CAA1C1的一個法向量…………11分
![]() …………12分
…………12分
由圖可知,二面角A―A1C―D的大小為![]() …………14分
…………14分


 手拉手全優練考卷系列答案
手拉手全優練考卷系列答案科目:高中數學 來源: 題型:
(09年海淀區期末文)(14分)
已知橢圓![]() A1、A2、B是橢圓的頂點(如圖),直線
A1、A2、B是橢圓的頂點(如圖),直線![]() 與橢圓交于異于橢圓頂點的P、Q兩點,且
與橢圓交于異于橢圓頂點的P、Q兩點,且![]() //A2B。若此橢圓的離心率為
//A2B。若此橢圓的離心率為![]()
(I)求此橢圓的方程;
(II)設直線A1P和直線BQ的傾斜角分別為![]() 是否為定值?若是,求出此定值;若不是,請說明理由。
是否為定值?若是,求出此定值;若不是,請說明理由。

查看答案和解析>>
科目:高中數學 來源: 題型:
(09年海淀區期末文)(14分)
某種家用電器每臺的銷售利潤與該電器的無故障使用時間有關,每臺這種家用電器若無故障使用時間不超過一年,則銷售利潤為0元,若無故障使用時間超過一年不超過三年,則銷售利潤為100元;若無故障使用時間超過三年,則銷售利潤為200元。
已知每臺該種電器的無故障使用時間不超過一年的概率為![]() 無故障使用時間超過一年不超過三年的概率為
無故障使用時間超過一年不超過三年的概率為![]()
(I)求銷售兩臺這種家用電器的銷售利潤總和為400元的概率;
(II)求銷售三臺這種家用電器的銷售利潤總和為300元的概率;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com