
已知球的直徑SC=4,A,B是該球球面上的兩點,AB=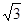 ,
,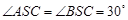 ,則棱錐S—ABC的體積為( )
,則棱錐S—ABC的體積為( )
A. | B.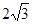 | C.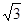 | D.1 |
C
解析試題分析:球心為點O,作AB中點D,連接OD,CD,說明SC是球的直徑,利用余弦定理,三角形的面積公式求出S△SCD,和棱錐的高AB,即可求出棱錐的體積。
設(shè)球心為點O,作AB中點D,連接OD,CD 因為線段SC是球的直徑,所以它也是大圓的直徑,則易得:∠SAC=∠SBC=90°所以在Rt△SAC中,SC=4,∠ASC="30°" 得:AC=2,SA=2
又在Rt△SBC中,SC=4,∠BSC="30°" 得:BC=2,SB=2 則:SA=SB,AC=BC
則:SA=SB,AC=BC
因為點D是AB的中點所以在等腰三角形ASB中,SD⊥AB且SD=
在等腰三角形CAB中,CD⊥AB且CD=
又SD交CD于點D 所以:AB⊥平面SCD 即:棱錐S-ABC的體積:V= AB•S△SCD,
AB•S△SCD,
因為:SD= ,CD=
,CD= ,SC="4" 所以由余弦定理得:cos∠SDC=(SD2+CD2-SC2)
,SC="4" 所以由余弦定理得:cos∠SDC=(SD2+CD2-SC2)
則:sin∠SDC=
由三角形面積公式得△SCD的面積S= SD•CD•sin∠SDC="=3"
SD•CD•sin∠SDC="=3"
所以:棱錐S-ABC的體積:V= AB•S△SCD=
AB•S△SCD=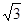 ,故選C
,故選C
考點:考查了簡單幾何體組合體的運用。
點評:本題是中檔題,考查球的內(nèi)接棱錐的體積的求法,考查空間想象能力,計算能力,有難度的題目,常考題型.


科目:高中數(shù)學(xué) 來源: 題型:單選題
如圖,一個簡單空間幾何體的三視圖其主視圖與側(cè)視圖都是邊長為2的正三角形,俯視圖輪廓為正方形,則此幾何體的側(cè)面積是
A. | B.12 |
C. | D.8 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
已知球的半徑為2,相互垂直的兩個平面分別截球面得兩個圓,若兩圓的公共弦長為2,則兩圓的圓心距等于( )
| A.1 | B.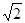 | C.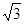 | D.2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
將正方形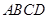 沿對角線
沿對角線 折成直二面角
折成直二面角 ,有如下四個結(jié)論:
,有如下四個結(jié)論:
① ⊥
⊥ ;②△
;②△ 是等邊三角形;③
是等邊三角形;③ 與平面
與平面 所成的角為60°;④
所成的角為60°;④ 與
與 所成的角為60°.其中錯誤的結(jié)論是( )
所成的角為60°.其中錯誤的結(jié)論是( )
| A.① | B.② | C.③ | D.④ |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com