
某煤礦發生透水事故時,作業區有若干人員被困.救援隊從入口進入之后有 兩條巷道通往作業區(如下圖),
兩條巷道通往作業區(如下圖), 巷道有
巷道有 三個易堵塞點,各點被堵塞的概率都是
三個易堵塞點,各點被堵塞的概率都是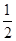 ;
; 巷道有
巷道有 兩個易堵塞點,被堵塞的概率分別為
兩個易堵塞點,被堵塞的概率分別為 .
.
(1)求 巷道中,三個易堵塞點最多有一個被堵塞的概率;
巷道中,三個易堵塞點最多有一個被堵塞的概率;
(2)若 巷道中堵塞點個數為
巷道中堵塞點個數為 ,求
,求 的分布列及數學期望
的分布列及數學期望 ,并按照"平均堵塞點少的巷道是較好的搶險路線"的標準,請你幫助救援隊選擇一條搶險路線,并說明理由.
,并按照"平均堵塞點少的巷道是較好的搶險路線"的標準,請你幫助救援隊選擇一條搶險路線,并說明理由.
(1)三個易堵塞點最多有一個被堵塞的概率為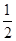 ;(2)選擇
;(2)選擇 巷道為搶險路線為好,該巷道平均堵塞點少.
巷道為搶險路線為好,該巷道平均堵塞點少.
解析試題分析:(1)
科目:高中數學
來源:
題型:解答題
商場銷售的某種飲品每件售價為36元,成本為20元.對該飲品進行促銷:顧客每購買一件,當即連續轉動三次如圖所示轉盤,每次停止后指針向一個數字,若三次指向同一個數字,獲一等獎;若三次指向的數字是連號(不考慮順序),獲二等獎;其他情況無獎.
科目:高中數學
來源:
題型:解答題
某中學在高一開設了數學史等4門不同的選修課,每個學生必須選修,且只能從中選一門.該校高一的3名學生甲、乙、丙對這4門不同的選修課的興趣相同.
科目:高中數學
來源:
題型:解答題
如圖,從A1(1,0,0)、A2(2,0,0)、B1(0,1,0)、B2(0,2,0)、C1(0,0,1)、C2(0,0,2)這6個點中隨機選取3個點,將這3個點及原點O兩兩相連構成一個“立體”,記該“立體”的體積為隨機變量V(如果選取的3個點與原點在同一個平面內,此時“立體”的體積V=0).
科目:高中數學
來源:
題型:解答題
黃山旅游公司為了體現尊師重教,在每年暑假期間對來黃山旅游的全國各地教師和學生,憑教師證和學生證實行購買門票優惠.某旅游公司組織有22名游客的旅游團到黃山旅游,其中有14名教師和8名學生.但是只有10名教師帶了教師證,6名學生帶了學生證.
科目:高中數學
來源:
題型:解答題
對某電子元件進行壽命追蹤調查,所得情況如右頻率分布直方圖.
科目:高中數學
來源:
題型:解答題
小波以游戲方式決定是參加學校合唱團還是參加學校排球隊,游戲規則為:以0為起點,再從
科目:高中數學
來源:
題型:解答題
甲乙兩人進行乒乓球比賽,各局相互獨立,約定每局勝者得1分,負者得0分,如果兩人比賽五局,乙得1分與得2分的概率恰好相等.
科目:高中數學
來源:
題型:解答題
一盒中裝有零件12個,其中有9個正品,3個次品,從中任取一個,如果每次取出次品就不再放回去,再取一個零件,直到取得正品為止.求在取得正品之前已取出次品數的期望.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區 巷道中,三個易堵塞點最多有一個被堵塞的概率
巷道中,三個易堵塞點最多有一個被堵塞的概率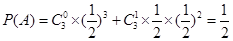 ;
;
(2)若 巷道中堵塞點個數為
巷道中堵塞點個數為 ,先寫出
,先寫出 的分布列,根據分布列求出數學期望
的分布列,根據分布列求出數學期望 ,同樣的方法求出
,同樣的方法求出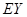 ,而
,而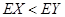 ,所以選擇
,所以選擇 巷道為搶險路線為好.
巷道為搶險路線為好.
試題解析:(1)設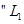 巷道中,三個易堵塞點最多有一個被堵塞
巷道中,三個易堵塞點最多有一個被堵塞 為事件
為事件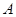
則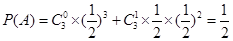
(2)依題意, 的可能取值為0,1,2
的可能取值為0,1,2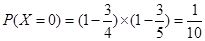
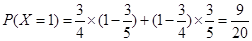
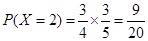
所以,隨機變量 的分布列為:
的分布列為:
0 1 2 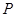
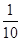
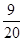
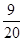
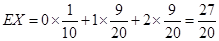
(方法一)設 巷道中堵塞點個數為
巷道中堵塞點個數為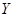 ,則
,則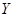 的可能取值為0,1,2,3
的可能取值為0,1,2,3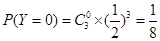
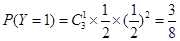
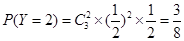
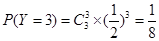
所以,隨機變量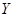 的分布列為:
的分布列為: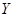
0 1 2 3 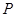
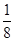


芝麻開花領航新課標中考方略系列答案
考點專項突破系列答案
核心考點全解系列答案
暑假作業哈薩克文系列答案
七彩練霸系列答案
紅對勾閱讀完形系列答案
考易通大試卷系列答案
奪冠金卷考點梳理全優卷系列答案
孟建平中考錯題本系列答案
輕松過關優選卷系列答案
(1)求一顧客一次購買兩件該飲品,至少有一件獲得獎勵的概率;
(2)若獎勵為返還現金,一等獎獎金數是二等獎的2倍,統計表明:每天的銷售y(件)與一等獎的獎金額x(元)的關系式為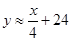 ,問x設定為多少最佳?并說明理由.
,問x設定為多少最佳?并說明理由.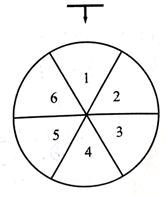
(1)求3個學生選擇了3門不同的選修課的概率;
(2)求恰有2門選修課這3個學生都沒有選擇的概率;
(3)設隨機變量X為甲、乙、丙這三個學生選修數學史這門課的人數,求X的分布列.
(1)求V=0的概率;
(2)求V的分布列及數學期望E(V).
(1)在該旅游團中隨機采訪3名游客,求恰有1人持有教師證且持有學生證者最多1人的概率;
(2)在該團中隨機采訪3名學生,設其中持有學生證的人數為隨機變量ξ,求ξ的分布列.
(1)圖中縱坐標 處刻度不清,根據圖表所提供的數據還原
處刻度不清,根據圖表所提供的數據還原 ;
;
(2)根據圖表的數據按分層抽樣,抽取 個元件,壽命為
個元件,壽命為 之間的應抽取幾個;
之間的應抽取幾個;
(3)從(2)中抽出的壽命落在 之間的元件中任取
之間的元件中任取 個元件,求事件“恰好有一個壽命為
個元件,求事件“恰好有一個壽命為 ,一個壽命為
,一個壽命為 ”的概率.
”的概率. ,
, (如圖)這8個點中任取兩點分別分終點得到兩個向量,記這兩個向量的數量積為X。若X=0就參加學校合唱團,否則就參加學校排球隊。
(如圖)這8個點中任取兩點分別分終點得到兩個向量,記這兩個向量的數量積為X。若X=0就參加學校合唱團,否則就參加學校排球隊。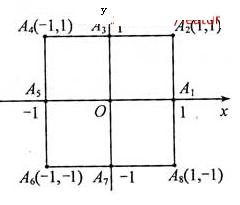
(1)求小波參加學校合唱團的概率;
(2)求X的分布列和數學期望.
求乙在每局中獲勝的概率為多少?
假設比賽進行到有一人比對方多2分或打滿6局時停止,用 表示比賽停止時已打局數,求
表示比賽停止時已打局數,求 的期望
的期望 .
.
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號