
商場銷售的某種飲品每件售價為36元,成本為20元.對該飲品進行促銷:顧客每購買一件,當即連續轉動三次如圖所示轉盤,每次停止后指針向一個數字,若三次指向同一個數字,獲一等獎;若三次指向的數字是連號(不考慮順序),獲二等獎;其他情況無獎.
(1)求一顧客一次購買兩件該飲品,至少有一件獲得獎勵的概率;
(2)若獎勵為返還現金,一等獎獎金數是二等獎的2倍,統計表明:每天的銷售y(件)與一等獎的獎金額x(元)的關系式為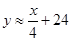 ,問x設定為多少最佳?并說明理由.
,問x設定為多少最佳?并說明理由.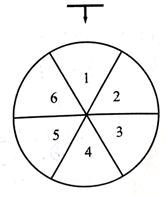
(1)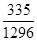 ;(2)x設定為48(元)為最佳.
;(2)x設定為48(元)為最佳.
解析試題分析:本題主要考查隨機事件的概率、離散型隨機變量的數學期望、配方法求函數最值等基礎知識,考查學生的分析問題解決問題的能力、計算能力、轉化能力.第一問,先利用活動法則分2種情況分別求出一顧客購買一件飲品獲得一等獎和二等獎的概率,2個結果相加得到一顧客購買一件飲品獲獎的概率,用間接法在所有概率中去掉2件都沒有獲獎的概率即可;第二問,先求顧客購買一件飲品所得的獎金額的數學期望,用每件售價-每件的成本-發放的獎金額=每件所得利潤,再用這個結果乘以一天賣出的總件數得一天的總利潤,再用配方法求函數最值.
(1)記事件:“一顧客購買一件飲品獲得i等獎”為Ai,i=1,2,則
P(A1)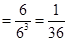 ,P(A2)=
,P(A2)=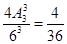 ,
,
則一顧客一次購買一件飲品獲得獎勵的概率為
P(A1+A2)=P(A1)+P(A2)=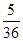 . 4分
. 4分
故一顧客一次購買兩件飲品,至少有一件獲得獎勵的概率
p=1-(1-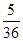 )2=
)2=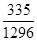 . 6分
. 6分
(2)設一顧客每購買一件飲品所得獎金額為X元,則X的可能取值為x,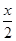 ,0.
,0.
由(1)得P(X=x)= ,P(X=
,P(X=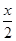 )=
)=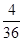 ,E(x)=
,E(x)=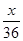 +
+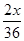 =
=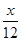 . 9分
. 9分
該商場每天銷售這種飲品所得平均利潤
Y=y[(36-20)-E(x)]=(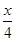 +24)(16-
+24)(16-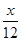 )=-
)=-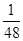 (x-48)2+432.
(x-48)2+432.
當x=48時,Y最大.故x設定為48(元)為最佳. 12分
考點:隨機事件的概率、離散型隨機變量的數學期望、配方法求函數最值.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:高中數學 來源: 題型:解答題
某種玫瑰花,進貨商當天以每支1元從鮮花批發商店購進,以每支2元售出.若當天賣不完,剩余的玫瑰花批發商店以每支0.5元的價格回收.根據市場統計,得到這個季節的日銷售量X(單位:支)的頻率分布直方圖(如圖所示),將頻率視為概率.(12分)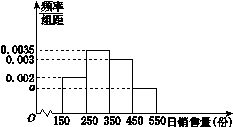
(1)求頻率分布直方圖中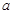 的值;
的值;
(2)若進貨量為 (單位支),當n≥X時,求利潤Y的表達式;
(單位支),當n≥X時,求利潤Y的表達式;
(3)若當天進貨量n=400,求利潤Y的分布列和數學期望E(Y)(統計方法中,同一組數據常用該組區間的中點值作為代表).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在一塊耕地上種植一種作物,每季種植成本為1000元,此作物的市場價格和這塊地上
的產量均具有隨機性,且互不影響,其具體情況如下表:

(1)設 表示在這塊地上種植1季此作物的利潤,求
表示在這塊地上種植1季此作物的利潤,求 的分布列;
的分布列;
(2)若在這塊地上連續3季種植此作物,求這3季中至少有2季的利潤不少于2000元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
第十二屆全國人民代表大會第二次會議和政協第十二屆全國委員會第二次會議,2014年3月在北京召開.為了做好兩會期間的接待服務工作,中國人民大學學生實踐活動中心從7名學生會干部(其中男生4人,女生3人)中選3人參加兩會的志愿者服務活動.
(1)所選3人中女生人數為 ,求
,求 的分布列及數學期望:
的分布列及數學期望:
(2)在男生甲被選中的情況下,求女生乙也被選中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一批產品需要進行質量檢驗,質檢部門規定的檢驗方案是:先從這批產品中任取3件作檢驗,若3件產品都是合格品,則通過檢驗;若有2件產品是合格品,則再從這批產品中任取1件作檢驗,這1件產品是合格品才能通過檢驗;若少于2件合格品,則不能通過檢驗,也不再抽檢. 假設這批產品的合格率為80%,且各件產品是否為合格品相互獨立.
(1)求這批產品通過檢驗的概率;
(2)已知每件產品檢驗費為125元,并且所抽取的產品都要檢驗,記這批產品的檢驗費為 元,求
元,求 的概率分布及數學期望.
的概率分布及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
隨機抽取某中學甲、乙兩班各10名同學,測量他們的身高(單位:cm),獲得身高數據的莖葉圖如下圖.
(1)根據莖葉圖判斷哪個班的平均身高較高;
(2)計算甲班的樣本方差;
(3)現從乙班這10名同學中隨機抽取兩名身高不低于173 cm的同學,求身高為176 cm的同學被抽中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某中學將100名高一新生分成水平相同的甲、乙兩個“平行班”,每班50人.陳老師采用A、B兩種不同的教學方式分別在甲、乙兩個班級進行教改實驗.為了了解教學效果,期末考試后,陳老師分別從兩個班級中各隨機抽取20名學生的成績進行統計,作出莖葉圖如下.記成績不低于90分者為“成績優秀”.
| 甲 | | 乙 |
| 6 | 9 | 3 6 7 9 9 |
| 9 5 1 0 | 8 | 0 1 5 6 |
| 9 9 4 4 2 | 7 | 3 4 5 8 8 8 |
| 8 8 5 1 1 0 | 6 | 0 7 7 |
| 4 3 3 2 | 5 | 2 5 |
| | 甲班(A方式) | 乙班(B方式) | 總計 |
| 成績優秀 | | | |
| 成績不優秀 | | | |
| 總計 | | | |
 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某煤礦發生透水事故時,作業區有若干人員被困.救援隊從入口進入之后有 兩條巷道通往作業區(如下圖),
兩條巷道通往作業區(如下圖), 巷道有
巷道有 三個易堵塞點,各點被堵塞的概率都是
三個易堵塞點,各點被堵塞的概率都是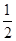 ;
; 巷道有
巷道有 兩個易堵塞點,被堵塞的概率分別為
兩個易堵塞點,被堵塞的概率分別為 .
.
(1)求 巷道中,三個易堵塞點最多有一個被堵塞的概率;
巷道中,三個易堵塞點最多有一個被堵塞的概率;
(2)若 巷道中堵塞點個數為
巷道中堵塞點個數為 ,求
,求 的分布列及數學期望
的分布列及數學期望 ,并按照"平均堵塞點少的巷道是較好的搶險路線"的標準,請你幫助救援隊選擇一條搶險路線,并說明理由.
,并按照"平均堵塞點少的巷道是較好的搶險路線"的標準,請你幫助救援隊選擇一條搶險路線,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(2011•山東)甲、乙兩校各有3名教師報名支教,期中甲校2男1女,乙校1男2女.
(1)若從甲校和乙校報名的教師中各任選1名,寫出所有可能的結果,并求選出的2名教師性別相同的概率;
(2)若從報名的6名教師中任選2名,寫出所有可能的結果,并求選出的2名教師來自同一學校的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com