
已知函數f(x)=-x2+2ax+1-a在x∈[0,1]時有最大值2,求a的值.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
某市環保部門對市中心每天環境污染情況進行調查研究,發現一天中環境污染指數 與時刻
與時刻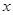 (時)的關系為
(時)的關系為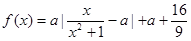 ,
, ,其中
,其中 是與氣象有關的參數,且
是與氣象有關的參數,且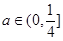 ,用每天
,用每天 的最大值作為當天的污染指數,記作
的最大值作為當天的污染指數,記作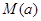 .
.
(1)令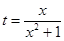 ,
, ,求
,求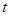 的取值范圍;
的取值范圍;
(2)按規定,每天的污染指數不得超過2,問目前市中心的污染指數是否超標?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如果n件產品中任取一件樣品是次品的概率為 ,則認為這批產品中有
,則認為這批產品中有 件次品。某企業的統計資料顯示,產品中發生次品的概率p與日產量n滿足
件次品。某企業的統計資料顯示,產品中發生次品的概率p與日產量n滿足
 ,有已知每生產一件正品可贏利a元,如果生產一件次品,非但不能贏利,還將損失
,有已知每生產一件正品可贏利a元,如果生產一件次品,非但不能贏利,還將損失 元(
元( ).
).
(1)求該企業日贏利額 的最大值;
的最大值;
(2)為保證每天的贏利額不少于日贏利額最大值的50%,試求該企業日產量的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
請你設計一個包裝盒,如圖所示, 是邊長為
是邊長為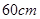 的正方形硬紙片,切去陰影部分所示的四個全等的等腰直角三角形,再沿虛線折起,使得
的正方形硬紙片,切去陰影部分所示的四個全等的等腰直角三角形,再沿虛線折起,使得 四個點重合于圖中的點P,正好形成一個正四棱柱形狀的包裝盒,
四個點重合于圖中的點P,正好形成一個正四棱柱形狀的包裝盒, 在
在 上是被切去的等腰直角三角形斜邊的兩個端點,設
上是被切去的等腰直角三角形斜邊的兩個端點,設 .
.
(1)若廣告商要求包裝盒側面積 最大,試問
最大,試問 應取何值?
應取何值?
(2)若廣告商要求包裝盒容積 最大,試問
最大,試問 應取何值?并求出此時包裝盒的高與底面邊長的比值.
應取何值?并求出此時包裝盒的高與底面邊長的比值.

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某村莊擬修建一個無蓋的圓柱形蓄水池(不計厚度).設該蓄水池的底面半徑為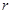 米,高為
米,高為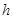 米,體積為
米,體積為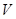 立方米.假設建造成本僅與表面積有關,側面積的建造成本為100元/平方米,底面的建造成本為160元/平方米,該蓄水池的總建造成本為
立方米.假設建造成本僅與表面積有關,側面積的建造成本為100元/平方米,底面的建造成本為160元/平方米,該蓄水池的總建造成本為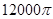 元(
元(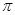 為圓周率).
為圓周率).
(1)將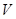 表示成
表示成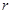 的函數
的函數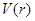 ,并求該函數的定義域;
,并求該函數的定義域;
(2)討論函數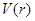 的單調性,并確定
的單調性,并確定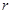 和
和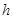 為何值時該蓄水池的體積最大.
為何值時該蓄水池的體積最大.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(2011•湖北)(1)已知函數f(x)=lnx﹣x+1,x∈(0,+∞),求函數f(x)的最大值;
(2)設a1,b1(k=1,2…,n)均為正數,證明:
①若a1b1+a2b2+…anbn≤b1+b2+…bn,則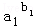
 …
…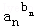 ≤1;
≤1;
②若b1+b2+…bn=1,則 ≤
≤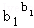
 …
…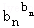 ≤b12+b22+…+bn2.
≤b12+b22+…+bn2.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com