
已知 為等比數列,
為等比數列,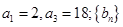 是等差數列,
是等差數列,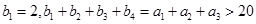
(Ⅰ)求數列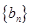 的通項公式及前
的通項公式及前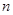 項和
項和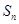 ;
;
(2)設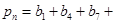
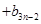 ,
,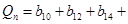
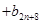 ,其中
,其中 ,試比較
,試比較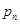 與
與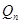 的大小,并加以證明.
的大小,并加以證明.
(Ⅰ)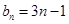 ,
,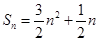 ;(Ⅱ)當
;(Ⅱ)當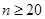 時,
時,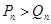 ;當
;當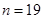 時,
時,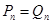 ;當
;當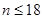 時,
時, .
.
解析試題分析:(Ⅰ)求數列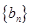 的通項公式及前
的通項公式及前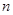 項和
項和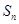 ,由已知
,由已知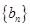 是等差數列,且
是等差數列,且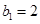 ,只需求出公差
,只需求出公差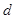 即可,由已知
即可,由已知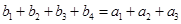 ,且
,且 為等比數列,
為等比數列,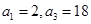 ,只需求出公比
,只需求出公比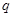 即可,由
即可,由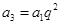 得,
得,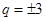 ,討論是否符合條件
,討論是否符合條件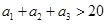 ,從而得
,從而得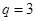 ,這樣問就可以解決;(Ⅱ)設
,這樣問就可以解決;(Ⅱ)設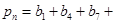
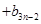 ,
,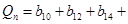
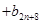 ,其中
,其中 ,試比較
,試比較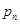 與
與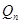 的大小,關鍵是求出
的大小,關鍵是求出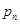 與
與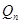 的關系式,由已知
的關系式,由已知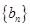 是等差數列,由(Ⅰ)知
是等差數列,由(Ⅰ)知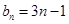 ,即可寫出
,即可寫出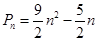 ,
, ,兩式作差得
,兩式作差得 ,討論即可.
,討論即可.
試題解析:(Ⅰ)設 的公比為
的公比為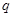 ,由
,由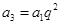 得,
得,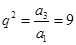 ,
,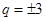 。 1分
。 1分
當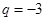 時,
時,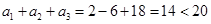 ,這與
,這與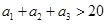 矛盾 2分
矛盾 2分
當 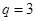 時,
時, ,符合題意。 3分
,符合題意。 3分
設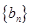 的公差為
的公差為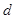 ,由
,由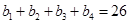 ,得:
,得: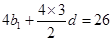
又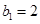
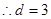
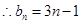 5分
5分
所以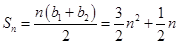 7分
7分
(Ⅱ)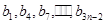 組成公差為
組成公差為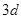 的等差數列,所以
的等差數列,所以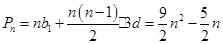 8分
8分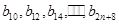 組成公差為
組成公差為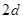 的等差數列, 所以
的等差數列, 所以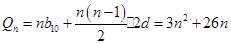
 10分
10分
故當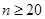 時,
時,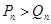 ;當
;當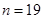 時,
時,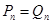 ;當
;當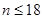 時,
時, 12分
12分
考點:等比數列,等差數列的通項公式,等差數列的前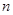 項和
項和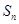 ,比較大小.
,比較大小.


 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案科目:高中數學 來源: 題型:解答題
設各項均為正數的數列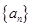 的前
的前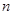 項和為
項和為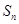 ,滿足
,滿足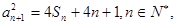 且
且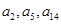 恰好是等比數列
恰好是等比數列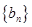 的前三項.
的前三項.
(Ⅰ)求數列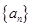 、
、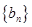 的通項公式;
的通項公式;
(Ⅱ)記數列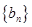 的前
的前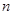 項和為
項和為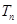 ,若對任意的
,若對任意的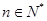 ,
,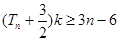 恒成立,求實數
恒成立,求實數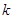 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設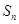 是數列
是數列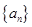 的前
的前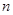 項和,對任意
項和,對任意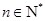 都有
都有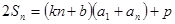 成立, (其中
成立, (其中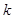 、
、 、
、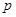 是常數).
是常數).
(1)當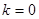 ,
,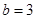 ,
,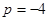 時,求
時,求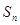 ;
;
(2)當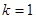 ,
,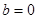 ,
,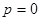 時,
時,
①若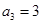 ,
,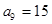 ,求數列
,求數列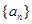 的通項公式;
的通項公式;
②設數列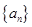 中任意(不同)兩項之和仍是該數列中的一項,則稱該數列是“
中任意(不同)兩項之和仍是該數列中的一項,則稱該數列是“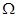 數列”.
數列”.
如果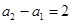 ,試問:是否存在數列
,試問:是否存在數列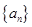 為“
為“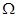 數列”,使得對任意
數列”,使得對任意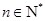 ,都有
,都有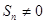 ,且
,且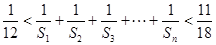 .若存在,求數列
.若存在,求數列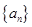 的首項
的首項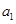 的所
的所
有取值構成的集合;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
現在市面上有普通型汽車(以汽油為燃料)和電動型汽車兩種。某品牌普通型汽車車價為12萬元,第一年汽油的消費為6000元,隨著汽油價格的不斷上升,汽油的消費每年以20%的速度增長。其它費用(保險及維修費用等)第一年為5000元,以后每年遞增2000元。而電動汽車由于節能環保,越來越受到社會認可。某品牌電動車在某市上市,車價為25萬元,購買時一次性享受國家補貼價6萬元和該市市政府補貼價4萬元。電動汽車動力不靠燃油,而靠電池。電動車使用的普通鋰電池平均使用壽命大約兩年(也即兩年需更換電池一次),電池價格為1萬元,電動汽車的其它費用每年約為5000元。
求使用 年,普通型汽車的總耗資費
年,普通型汽車的總耗資費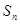 (萬元)的表達式
(萬元)的表達式
(總耗資費=車價+汽油費+其它費用)
比較兩種汽車各使用10年的總耗資費用
(參考數據: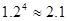
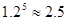
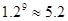
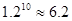 )
)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列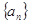 中,
中,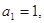 且點
且點 在直線
在直線 上。
上。
(1)求數列 的通項公式;
的通項公式;
(2)若函數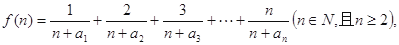 求函數
求函數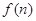 的最小值;
的最小值;
(3)設 表示數列
表示數列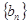 的前項和.試問:是否存在關于
的前項和.試問:是否存在關于 的整式
的整式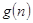 ,使得
,使得 對于一切不小于2的自然數
對于一切不小于2的自然數 恒成立?若存在,寫出
恒成立?若存在,寫出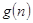 的解析式,并加以證明;若不存在,試說明理由。
的解析式,并加以證明;若不存在,試說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知等差數列{an}的前n項和為Sn,公差d≠0,且 成等比數列.
成等比數列.
(1)求數列{an}的通項公式;
(2)設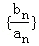 是首項為1,公比為3的等比數列,求數列{bn}的前n項和Tn.
是首項為1,公比為3的等比數列,求數列{bn}的前n項和Tn.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com