中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

（本題滿分8分）
從裝有6個紅球、4個白球的袋中隨機取出3個球，設其中有個紅球，求隨機變量的分布列．

練習冊系列答案
相關習題

科目：高中數學 來源：2012-2013學年浙江省溫州市高三第一次適應性測試理科數學試卷（解析版） 題型：解答題

（本題滿分14分）

從裝有大小相同的2個紅球和6個白球的袋子中，每摸出2個球為一次試驗，直到摸出的球中有紅球（不放回），則試驗結束．

（Ⅰ）求第一次試驗恰摸到一個紅球和一個白球概率；

（Ⅱ）記試驗次數為，求的分布列及數學期望．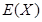

 

查看答案和解析>>

科目：高中數學 來源：2011-2012學年浙江省桐鄉市高三10月月考理科數學 題型：解答題

（本題滿分14分）從裝有2只紅球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同．

（Ⅰ）若抽取后又放回,抽取3次,求恰好抽到2次為紅球的概率;

（Ⅱ）若抽取后不放回,設抽完紅球所需的次數為,求的分布列及期望．

 

查看答案和解析>>

科目：高中數學 來源：2014屆浙江省臺州市高一上學期期末考試數學試卷 題型：解答題

（本題滿分8分）為了估計某校的某次數學期末考試情況，現從該校參加考試的600名學生中隨機抽出60名學生，其成績（百分制）均在上．將這些成績分成六段，，…，后得到如下部分頻率分布直方圖．

 

 

（Ⅰ）求抽出的60名學生中分數在內的人數；

（Ⅱ）若規定成績不小于85分為優秀，則根據頻  率分布直方圖，估計該校的優秀人數．

 

查看答案和解析>>

科目：高中數學 來源：2010年上海市盧灣區高三第二次模擬考試數學卷（文） 題型：解答題

（本題滿分18分）本題共有3個小題，第1小題滿分4分，第2小題滿分6分，第3小題滿分8分．

從數列中取出部分項，并將它們按原來的順序組成一個數列，稱之為數列的一個子數列．

     設數列是一個首項為、公差為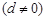的無窮等差數列．

（1）若，，成等比數列，求其公比．

（2）若，從數列中取出第2項、第6項作為一個等比數列的第1項、第2項，試問該數列是否為的無窮等比子數列，請說明理由．

（3）若，從數列中取出第1項、第項（設）作為一個等比數列的第1項、第2項．求證：當為大于1的正整數時，該數列為的無窮等比子數列．

 

查看答案和解析>>

同步練習冊答案