
橢圓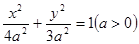 的左焦點為
的左焦點為 ,直線
,直線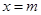 與橢圓相交于點
與橢圓相交于點 、
、 ,當
,當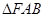 的周長最大時,
的周長最大時,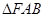 的面積是____________.
的面積是____________.

解析試題分析:設橢圓的右焦點為E.如圖: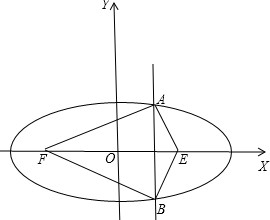
由橢圓的定義得:△FAB的周長:AB+AF+BF=AB+(4a-AE)+(4a-BE)=8a+AB-AE-BE;
∵AE+BE≥AB;
∴AB-AE-BE≤0,當AB過點E時取等號;
∴AB+AF+BF=8a+AB-AE-BE≤8a;
即直線x=m過橢圓的右焦點E時△FAB的周長最大;
此時△FAB的高為:EF=2a.
此時直線x=m=c=a;
把x=a代入橢圓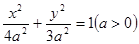
的方程得:y=±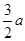 .
.
∴AB=3a.
所以:△FAB的面積等于:S△FAB=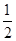 ×3a×2a=
×3a×2a= .
.
考點:本題主要考查橢圓的幾何性質,直線與橢圓的位置關系.
點評:在解決涉及到圓錐曲線上的點與焦點之間的關系的問題中,圓錐曲線的定義往往是解題的突破口.解決本題的關鍵在于利用定義求出周長的表達式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com