
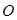 為坐標原點,
為坐標原點,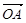 =(
=(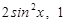 ),
),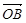 =(1,
=(1,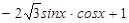 ),
), 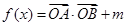 .
.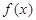 的定義域為[-
的定義域為[-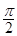 ,
,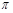 ],求y=
],求y=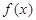 的單調遞增區間;
的單調遞增區間;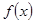 的定義域為[
的定義域為[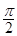 ,
,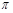 ],值域為[2,5],求
],值域為[2,5],求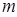 的值.
的值.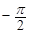 ,
,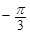 ],[
],[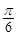 ,
, ] ;(2)m=1;
] ;(2)m=1;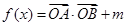 的解析式表示出來,這里要用到向量積的坐標運算,得到
的解析式表示出來,這里要用到向量積的坐標運算,得到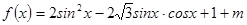 ,要求這類函數的單調區間要“降冪化同”,降冪即把高次冪降為一次冪,化同即化為同一個三角函數,“降冪化同”的時候要利用到倍角公式及輔助角公式,最后得到
,要求這類函數的單調區間要“降冪化同”,降冪即把高次冪降為一次冪,化同即化為同一個三角函數,“降冪化同”的時候要利用到倍角公式及輔助角公式,最后得到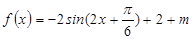 ,由正弦函數的單調性及函數的定義域即可得解;(2)由
,由正弦函數的單調性及函數的定義域即可得解;(2)由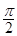 ≤x≤
≤x≤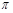 得
得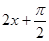 的取值范圍,從而得到
的取值范圍,從而得到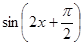 的取值范圍,最后得到
的取值范圍,最后得到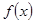 的取值范圍,而
的取值范圍,而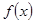 的取值范圍為
的取值范圍為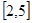 ,把求出來的
,把求出來的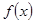 的取值范圍的兩個端點與
的取值范圍的兩個端點與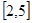 的兩個端點相等即可求出
的兩個端點相等即可求出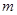 的取值。
的取值。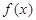 =
=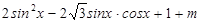
 =
=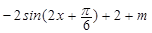 (4分)
(4分) (k∈Z),
(k∈Z),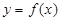 在
在 上的單調遞增區間為
上的單調遞增區間為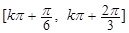 (k∈Z),
(k∈Z),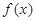 的定義域為[-
的定義域為[-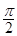 ,
,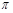 ],
],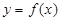 的增區間為:[
的增區間為:[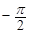 ,
,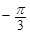 ],[
],[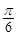 ,
, ] (7分)
] (7分)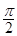 ≤x≤
≤x≤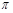 時,
時,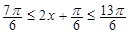 ,∴
,∴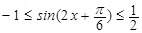 ,
,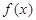 ≤4+m,∴
≤4+m,∴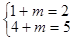
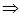 m=1 (12分)
m=1 (12分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com