
已知圓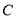 過點
過點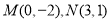 ,且圓心
,且圓心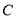 在直線
在直線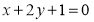 上。
上。
(I)求圓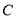 的方程;
的方程;
(II)問是否存在滿足以下兩個條件的直線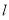 : ①斜率為
: ①斜率為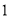 ;②直線被圓
;②直線被圓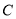 截得的弦為
截得的弦為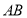 ,以
,以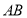 為直徑的圓
為直徑的圓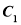 過原點. 若存在這樣的直線,請求出其方程;若不存在,說明理由.
過原點. 若存在這樣的直線,請求出其方程;若不存在,說明理由.
(I)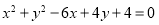 (II)存在,
(II)存在,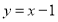 或
或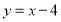
【解析】
試題分析:(I)用待定系數法求圓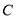 的方程,即先設出圓
的方程,即先設出圓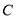 的標準式方程或一般式方程,然后根據已知條件列出方程組求出未知系數即可。(II)假設直線
的標準式方程或一般式方程,然后根據已知條件列出方程組求出未知系數即可。(II)假設直線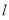 存在,其方程為
存在,其方程為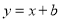 ,與圓的方程聯立 消去
,與圓的方程聯立 消去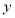 得到關于
得到關于 的一元二次方程,由韋達定理得到根與系數間的關系,因直線與圓由兩個交點故此一元二次方程的判別式應大于0。以
的一元二次方程,由韋達定理得到根與系數間的關系,因直線與圓由兩個交點故此一元二次方程的判別式應大于0。以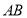 為直徑的圓
為直徑的圓 過原點即
過原點即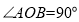 ,可轉化為直線
,可轉化為直線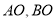 垂直斜率乘積等于
垂直斜率乘積等于 ,也可轉化為
,也可轉化為 ,還可轉化為直角三角形勾股定理即
,還可轉化為直角三角形勾股定理即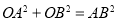 ,得到
,得到 。即可得到關于
。即可得到關于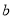 的方程,若方程有解則假設成立,否則假設不成立。
的方程,若方程有解則假設成立,否則假設不成立。
試題解析:【解析】
(1)設圓C的方程為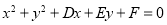
則 解得D= 6,E=4,F=4
解得D= 6,E=4,F=4
所以圓C方程為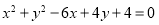 5分
5分
(2)設直線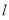 存在,其方程為
存在,其方程為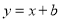 ,它與圓C的交點設為A
,它與圓C的交點設為A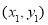 、B
、B
則由 得
得 (*)
(*)
∴  7分
7分
∴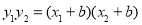 =
=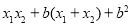 因為AB為直徑,所以,
因為AB為直徑,所以,
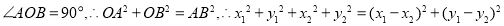
得 , 9分
, 9分
∴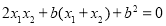 ,
,
即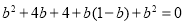 ,
,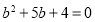 ,∴
,∴ 或
或 11分
11分
容易驗證 或
或 時方程(*)有實根.
時方程(*)有實根.
故存在這樣的直線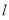 有兩條,其方程是
有兩條,其方程是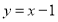 或
或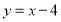 . 12分
. 12分
考點:圓的方程,直線和圓的位置關系,考查分析問題、解決問題的能力。


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2016屆安徽渦陽四中蒙城六中高一上學期期末聯考數學卷(解析版) 題型:選擇題
設m、n是兩條不同的直線, 是三個不同的平面,給出下列四個命題:
是三個不同的平面,給出下列四個命題:
①若 ,
, ,則
,則 ②若
②若 ,
, ,
, ,則
,則
③若 ,
, ,則
,則 ④若
④若 ,
, ,則
,則
其中正確命題的序號是 ( )
A.①和② B.②和③ C.③和④ D.①和④
查看答案和解析>>
科目:高中數學 來源:2016屆吉林省吉林市高一上期末檢測數學卷(解析版) 題型:填空題
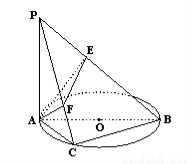
如圖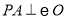 所在平面,
所在平面,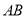 是
是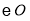 的直徑,
的直徑,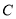 是
是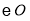 上一點,
上一點,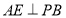 ,
,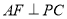 ,給出下列結論:①
,給出下列結論:①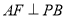 ; ②
; ②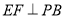 ;③
;③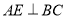 ; ④平面
; ④平面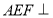 平面
平面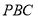 ⑤
⑤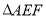 是直角三角形
是直角三角形
其中正確的命題的序號是
查看答案和解析>>
科目:高中數學 來源:2016屆上海浦東新區高一第一學期期末質量測試數學試卷(解析版) 題型:填空題
關于x的方程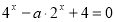 在
在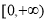 上有兩個不同的實數根,則實數a的取值范圍是___________.
上有兩個不同的實數根,則實數a的取值范圍是___________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com