
設函數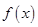 對任意
對任意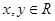 ,都有
,都有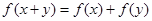 ,當
,當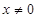 時,
時,
(1)求證: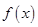 是奇函數;
是奇函數;
(2)試問:在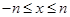 時
時  ,
,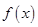 是否有最大值?如果有,求出最大值,如果沒有,說明理由.
是否有最大值?如果有,求出最大值,如果沒有,說明理由.
(3)解關于x的不等式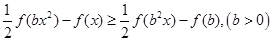
(1)詳見解析;(2)函數最大值為 ;(3)①
;(3)① ,則解為
,則解為 ;②
;② ,則解為
,則解為 ;③
;③ ,則無解.
,則無解.
解析試題分析:(1)要證明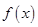 為奇函數,需要證明
為奇函數,需要證明 .如何利用所給條件變出這樣一個等式來?
.如何利用所給條件變出這樣一個等式來?
為了產生 ,令
,令 ,則
,則 .這時的
.這時的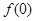 等于0嗎?如何求
等于0嗎?如何求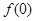 ?再設
?再設 可得
可得 ,從而問題得證.
,從而問題得證.
(2)一個連續函數在閉區間上必最大值的最小值.為了求函數的最值,就需要研究函數的單調性.研究單調性,第一,根據定義,第二利用導數.抽象函數研究單調性只能用定義.任取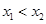 ,則
,則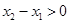 ,根據條件可得:
,根據條件可得: 即
即
所以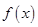 為減函數,那么函數在
為減函數,那么函數在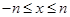 上的最大值為
上的最大值為 .
.
(3)有關抽象函數的不等式,都是利用單調性去掉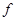 .首先要將不等式化為
.首先要將不等式化為 ,注意必須是左右各一項.在本題中,由題設可得
,注意必須是左右各一項.在本題中,由題設可得 ,
, 在R上為減函數
在R上為減函數 ,即
,即 .下面就解這個不等式.這個不等式中含有參數
.下面就解這個不等式.這個不等式中含有參數 ,故需要分情況討論.
,故需要分情況討論.
試題解析:(1)設 可得
可得 ,設
,設 ,則
,則
所以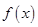 為奇函數.
為奇函數.
(2)任取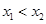 ,則
,則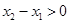 ,又
,又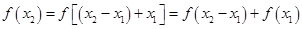
所以
所以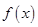 為減函數。
為減函數。
那么函數最大值為 ,
,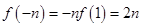 ,
,
所以函數最大值為 .
.
(3)由題設可知
即
可化為
即 ,
, 在R上為減函數
在R上為減函數 ,即
,即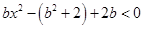 ,
,
① ,則解為
,則解為
② ,則解為
,則解為
③ ,則無解
,則無解
考點:1、抽象函數;2、函數的性質;3、解不等式.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案 應用題作業本系列答案
應用題作業本系列答案科目:高中數學 來源: 題型:解答題
已知函數 過點
過點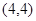 .
.
(1)求實數 ;
;
(2)將函數 的圖像向下平移1個單位,再向右平移
的圖像向下平移1個單位,再向右平移 個單位后得到函數
個單位后得到函數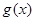 圖像,設函數
圖像,設函數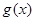 關于
關于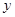 軸對稱的函數為
軸對稱的函數為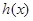 ,試求
,試求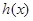 的解析式;
的解析式;
(3)對于定義在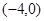 上的函數
上的函數 ,若在其定義域內,不等式
,若在其定義域內,不等式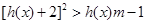 恒成立,求實數
恒成立,求實數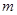 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某創業投資公司擬投資開發某種新能源產品,估計能獲得10萬元到1000萬元的投資收益.現準備制定一個對科研課題組的獎勵方案:獎金 (單位:萬元)隨投資收益
(單位:萬元)隨投資收益 (單位:萬元)的增加而增加,且獎金不超過9萬元,同時獎金不超過投資收益的20%.
(單位:萬元)的增加而增加,且獎金不超過9萬元,同時獎金不超過投資收益的20%.
(1)若建立函數 模型制定獎勵方案,試用數學語言表述該公司對獎勵函數
模型制定獎勵方案,試用數學語言表述該公司對獎勵函數 模型的基本要求,并分析函數
模型的基本要求,并分析函數 是否符合這個要求,并說明原因;
是否符合這個要求,并說明原因;
(2)若該公司采用函數 作為獎勵函數模型,試確定最小的正整數
作為獎勵函數模型,試確定最小的正整數 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com