
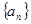 具有性質:①
具有性質:①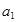 為正數;②對于任意的正整數
為正數;②對于任意的正整數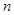 ,當
,當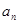 為偶數時,
為偶數時,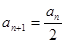 ;當
;當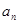 為奇數時,
為奇數時,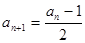
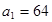 ,求數列
,求數列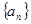 的通項公式;
的通項公式;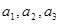 成等差數列,求
成等差數列,求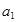 的值;
的值;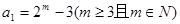 ,數列
,數列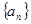 的前
的前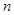 項和為
項和為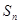 ,求證:
,求證: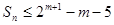
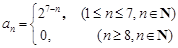 ;(2) 2;(3)證明見試題解析.
;(2) 2;(3)證明見試題解析.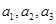
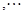 ,因為按照定義
,因為按照定義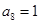 ,
,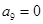 ,而此開始
,而此開始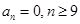 ,故可得出
,故可得出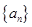 通項公式;(2)顯然
通項公式;(2)顯然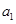 必須是整數,而且要計算
必須是整數,而且要計算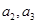 ,因此我們可以根據
,因此我們可以根據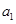 的值分類討論(分成四類
的值分類討論(分成四類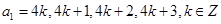 ).(3)
).(3)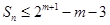 ,最好能求出
,最好能求出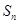 ,那么也就要求出數列
,那么也就要求出數列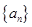 的各項,那么我們根據數列
的各項,那么我們根據數列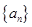 定義,由
定義,由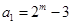 為奇數,則
為奇數,則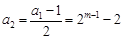 為偶數,
為偶數,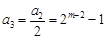 為奇數,接下來各項都是偶數,一起到某項為1,下面一項為0,以后全部為0.實際上項為1的項是第
為奇數,接下來各項都是偶數,一起到某項為1,下面一項為0,以后全部為0.實際上項為1的項是第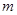 項,且
項,且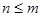 時
時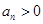 ,
,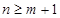 時
時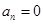 ,因此
,因此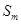 是最大的,但在計算
是最大的,但在計算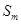 時,要注意當
時,要注意當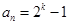 時,
時,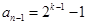 ,只要它不為0,就可繼續下去.
,只要它不為0,就可繼續下去.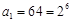 ,可得
,可得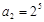 ,
,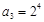 ,…,
,…,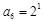 ,
,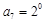 ,
,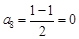 ,
,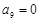 ,…,
,…,  的前7項成等比數列,從第8起數列的項均為0. (2分)
的前7項成等比數列,從第8起數列的項均為0. (2分) 的通項公式為
的通項公式為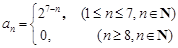 . (4分)
. (4分)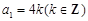 時,
時,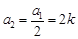 ,
,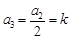 ,
,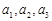 成等差數列,可知即
成等差數列,可知即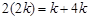 ,解得
,解得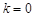 ,故
,故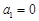 ;(舍去)
;(舍去) 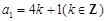 時,
時,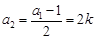 ,
,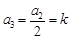 ,
,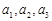 成等差數列,可知
成等差數列,可知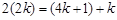 ,解得
,解得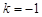 ,故
,故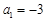 ;(舍去)(3分)
;(舍去)(3分)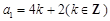 時,
時,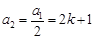 ,
,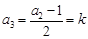 ,
,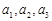 成等差數列,可知
成等差數列,可知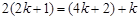 ,解得
,解得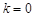 ,故
,故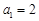 ;
;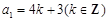 時,
時,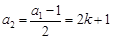 ,
,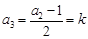 ,
,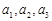 成等差數列,可知
成等差數列,可知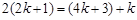 ,解得
,解得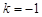 ,故
,故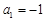 ;(舍去)
;(舍去)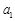 的值為2. (6分)
的值為2. (6分) (
(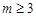 ),可得
),可得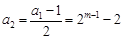 ,
,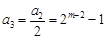 ,
,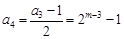 ,
,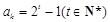 ,則
,則 是奇數,從而
是奇數,從而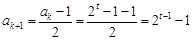 ,
,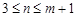 時,
時,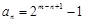 成立. (3分)
成立. (3分)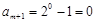 ,
,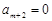 ,…
,…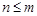 時,
時,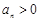 ;當
;當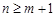 時,
時,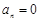 . (5分)
. (5分)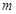 ,
,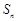 的最大值為
的最大值為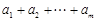
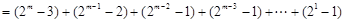
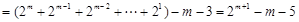 ,
,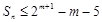 . (8分)
. (8分) 項和與最大值.
項和與最大值.

 優百分課時互動系列答案
優百分課時互動系列答案 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案科目:高中數學 來源:不詳 題型:解答題
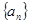 中,
中,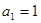 ,公差
,公差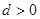 ,且它的第2項,第5項,第14項分別是等比數列
,且它的第2項,第5項,第14項分別是等比數列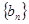 的第2項,第3項,第4項.
的第2項,第3項,第4項.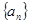 與
與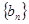 的通項公式;
的通項公式;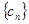 對任意自然數均有
對任意自然數均有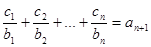 成立,求
成立,求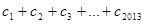 的值.
的值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com