
已知函數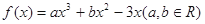 ,在點
,在點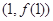 處的切線方程為
處的切線方程為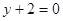 .
.
(Ⅰ)求函數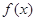 的解析式;
的解析式;
(Ⅱ)若對于區間 上任意兩個自變量的值
上任意兩個自變量的值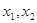 ,都有
,都有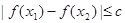 ,求實數
,求實數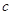 的最小值;
的最小值;
(Ⅲ)若過點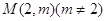 ,可作曲線
,可作曲線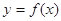 的三條切線,求實數
的三條切線,求實數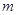 的取值范圍.
的取值范圍.
(1)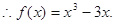
(2)4
(3)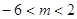
解析試題分析:(Ⅰ)
科目:高中數學
來源:
題型:解答題
設函數f(x)=x3-3ax2+3bx的圖像與直線12x+y-1=0相切于點(1,-11)。
科目:高中數學
來源:
題型:解答題
設函數
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
根據題意,得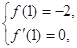 即
即
解得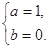
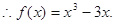
(Ⅱ)令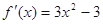
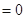 ,解得
,解得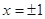
f(-1)=2, f(1)=-2,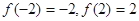
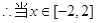 時,
時,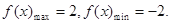
則對于區間[-2,2]上任意兩個自變量的值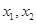 ,都有
,都有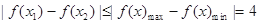
所以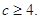 所以
所以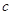 的最小值為4。
的最小值為4。
(Ⅲ)設切點為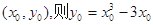
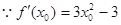 ,
, 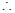 切線的斜率為
切線的斜率為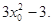
則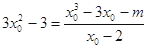
即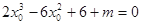 ,
,
因為過點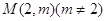 ,可作曲線
,可作曲線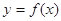 的三條切線
的三條切線
所以方程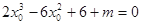 有三個不同的實數解
有三個不同的實數解
即函數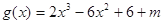 有三個不同的零點,
有三個不同的零點,
則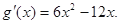
令
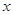
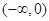
0 (0,2) 2 (2,+∞) 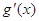
+ 0 — 0 + 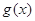

極大值 


五州圖書超越訓練系列答案
探究學案專項期末卷系列答案
暑假生活指導山東教育出版社系列答案
假期生活暑假安徽教育出版社系列答案
新課程暑假作業廣西師范大學出版社系列答案
高中暑假作業浙江教育出版社系列答案
少年素質教育報暑假作業系列答案
金太陽全A加系列答案
創新導學案新課標寒假假期自主學習訓練系列答案
超能學典暑假接力棒江蘇鳳凰少年兒童出版社系列答案
(1)求a,b的值;
(2)討論函數f(x)的單調性。 .
.
(1)若函數 圖像上的點到直線
圖像上的點到直線 距離的最小值為
距離的最小值為 ,求
,求 的值;
的值;
(2)關于 的不等式
的不等式 的解集中的整數恰有3個,求實數
的解集中的整數恰有3個,求實數 的取值范圍;
的取值范圍;
(3)對于函數 定義域上的任意實數
定義域上的任意實數 ,若存在常數
,若存在常數 ,使得
,使得 和
和 都成立,則稱直線
都成立,則稱直線 為函數
為函數 的
的
“分界線”.設 ,試探究
,試探究 是否存在“分界線”?若存在,求出“分界線”的方程,若不存在,請說明理由.
是否存在“分界線”?若存在,求出“分界線”的方程,若不存在,請說明理由.
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號