Question

設(shè)點P是雙曲線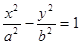上除頂點外的任意一點，F(xiàn)₁，F(xiàn)₂分別為左、右焦點，c 為半焦距，PF₁F₂的內(nèi)切圓與邊F₁F₂切于點M，求|F₁M|·|F₂M|=       

Answer 1

解析試題分析：解：根據(jù)從圓外一點向圓所引的兩條切線長相等可知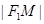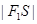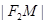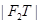：=，=|，|PS|=|PT|
①當P在雙曲線圖象的右支時，而根據(jù)雙曲線的定義可知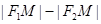
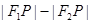==2a①；
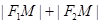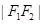而==2c②，
聯(lián)立①②解得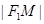： =a+c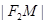， =c-a，所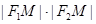=（a+c）（c-a）=c²-a²=b²；
②當P在雙曲線圖象的左支時，而根據(jù)雙曲線的定義可知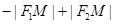
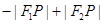==2a③；
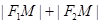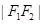而==2c④，
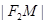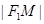聯(lián)立③④解得： =a+c，=c-a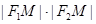，=（a+c）（c-a）=c²-a²=b²．
綜上，可得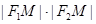=b²．
故答案為：b²
考點：雙曲線的性質(zhì)
點評：考查學生掌握雙曲線的基本性質(zhì)，靈活運用圓切線長定理化簡求值．做題時注意利用分類討論的數(shù)學思想