已知函數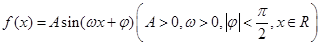
圖象的一部分如圖所示．
（1）求函數
的解析式；
（2）當
時，求函數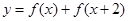
的最大值與最小值及相應的
的值．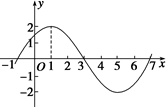
科目：高中數學 來源： 題型：解答題
已知A(x1,f(x1))，B(x2,f(x2))是函數f(x)=2sin(wx+j)(w＞0,
＜j＜0)圖象上的任意兩點，且角j的終邊經過點P(l，-
)，若|f(x1)-f(x2)|=4時，|x1-x2|的最小值為
.
(1)求函數f(x)的解析式；(2)求函數f(x)的單調遞增區間；(3)當x∈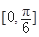
時，不等式mf(x)+2m≥f(x)恒成立，求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
；（2）
時，
，
時，
.
，
，從而可知
，再由圖象過點
可知
，結合條件中
即可得
，從而
，
可知
，
時，即
時，即
，∴
，
，α為第三象限角．
，
的值；
），tan2α的值．
，
，若函數
.
的最小正周期；
，求
值；
，求
，
的最小正周期及在區間
上的最大值和最小值；
，求
的值.
.
；
是第三象限角，且
，求
，
，且
.求：
的值；（2）
的值.
，其中
時，求
在區間
上的最大值與最小值；
，求
的值.
＝________.