
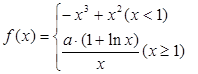 ,曲線
,曲線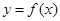 上是否存在兩點
上是否存在兩點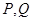 ,使得△
,使得△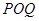 是以
是以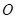 為直角頂點的直角三角形,且此三角形斜邊的中點在
為直角頂點的直角三角形,且此三角形斜邊的中點在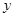 軸上.如果存在,求出實數
軸上.如果存在,求出實數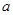 的范圍;如果不存在,說明理由.
的范圍;如果不存在,說明理由.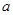 的取值范圍是
的取值范圍是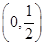 .
.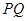 的中點在
的中點在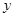 軸上這一條件進行轉化,確定點
軸上這一條件進行轉化,確定點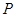 與點
與點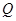 之間的關系,并將
之間的關系,并將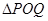 是以點
是以點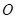 為直角頂點條件轉化為
為直角頂點條件轉化為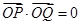 ,進行得到一個方程,然后就這個方程在定義域上是否有解對自變量的取值進行分類討論,進而求出參數
,進行得到一個方程,然后就這個方程在定義域上是否有解對自變量的取值進行分類討論,進而求出參數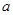 的取值范圍.
的取值范圍.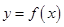 上存在兩點
上存在兩點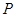 、
、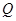 滿足題意,則
滿足題意,則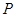 、
、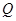 兩點只能在
兩點只能在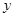 軸兩側,
軸兩側,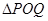 是以
是以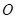 為直角頂點的直角三角形,所以
為直角頂點的直角三角形,所以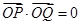 ,
,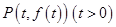 ,則由
,則由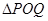 的斜邊的中點在
的斜邊的中點在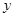 軸上知
軸上知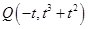 ,且
,且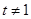 ,
,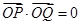 ,所以
,所以 (*)
(*)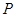 、
、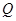 滿足題意等價于方程(*)是否有解問題,
滿足題意等價于方程(*)是否有解問題,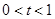 時,即
時,即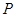 、
、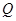 都在
都在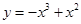 上,則
上,則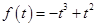 ,
,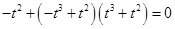 ,即
,即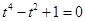 ,而此方程無實數解;
,而此方程無實數解;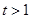 時,即
時,即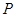 在
在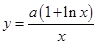 上,
上,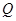 在
在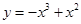 上,
上,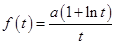 ,代入方程(*)得,
,代入方程(*)得,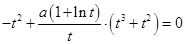 ,即
,即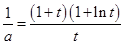 ,
, ,則
,則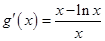 ,
,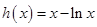 ,則
,則 ,所以
,所以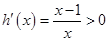 在
在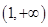 上恒成立,
上恒成立,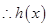 在
在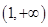 上單調遞增,
上單調遞增, ,從而
,從而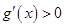 ,故
,故 在
在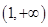 上也單調遞增,
上也單調遞增,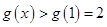 ,即
,即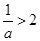 ,解得
,解得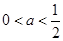 ,
,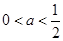 時,方程
時,方程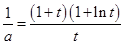 有解,即方程(*)有解,
有解,即方程(*)有解,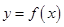 上總存在兩點
上總存在兩點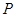 、
、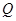 ,使得
,使得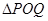 是以
是以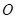 為直角頂點的直角三角形,
為直角頂點的直角三角形,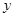 軸上,此時
軸上,此時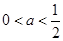 .
.

 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:高中數學 來源:不詳 題型:解答題
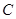 的圓心
的圓心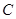 與點
與點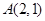 關于直線
關于直線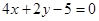 對稱,圓
對稱,圓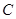 與直線
與直線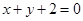 相切.
相切.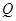 為圓
為圓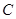 上的一個動點,若點
上的一個動點,若點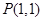 ,
,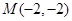 ,求
,求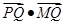 的最小值;
的最小值;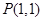 作兩條相異直線分別與圓
作兩條相異直線分別與圓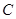 相交于
相交于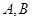 ,且直線
,且直線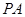 和直線
和直線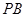 的傾斜角互補,
的傾斜角互補,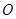 為坐標原點,試判斷直線
為坐標原點,試判斷直線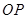 和
和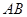 是否平行?請說明理由.
是否平行?請說明理由.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
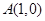 和點
和點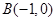 ,
,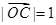 ,且
,且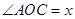 ,其中
,其中 為坐標原點.
為坐標原點.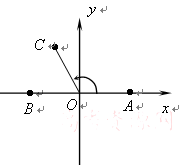
 ,設點
,設點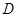 為線段
為線段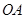 上的動點,求
上的動點,求 的最小值;
的最小值;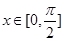 ,向量
,向量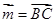 ,
,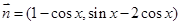 ,求
,求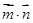 的最小值及對應的
的最小值及對應的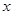 值.
值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com