(本小題共14分)
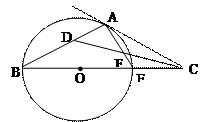
已知橢圓
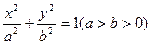
的離心率為
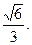
(I)若原點(diǎn)到直線
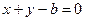
的距離為
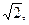
求橢圓的方程;
(II)設(shè)過橢圓的右焦點(diǎn)且傾斜角為
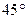
的直線
和橢圓交于
A,
B兩點(diǎn).
(i)當(dāng)

,求
b的值;
(ii)對(duì)于橢圓上任一點(diǎn)
M,若
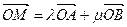
,求實(shí)數(shù)
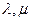
滿足的關(guān)系式.
(I)
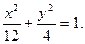
(II)(i)1
(ii)

(I)
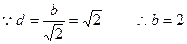
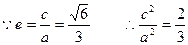

解得
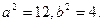
橢圓的方程為
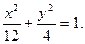
…………………………………………4分
(II)(i)

橢圓的方程可化為:

①
易知右焦點(diǎn)
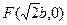
,據(jù)題意有AB:
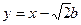
②
由①,②有:
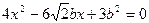
③
設(shè)
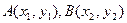
,
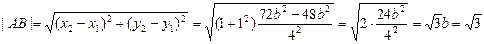
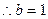
…………………………………………………………8分
(ii)顯然
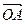
與
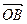
可作為平面向量的一組基底,由平面向量基本定理,對(duì)于這一平面內(nèi)的向量
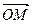
,有且只有一對(duì)實(shí)數(shù)λ,μ,使得等
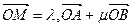
成立.
設(shè)M(
x,y),
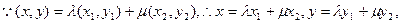
又點(diǎn)M在橢圓上,
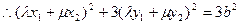
④
由③有:
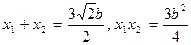
則


⑤
又A,B在橢圓上,故有
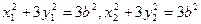
⑥
將⑥,⑤代入④可得:

………………………………14分
練習(xí)冊(cè)系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
(幾何證明選講選做題)已知PA是圓O的切點(diǎn),切點(diǎn)為A,PA=2.AC是圓O的直徑,PC與圓O交于B點(diǎn),PB=1,則圓O的半徑R=________.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖所示,
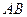
是
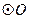
的直徑,
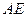
平分
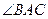
交
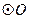
于點(diǎn)
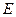
,過點(diǎn)
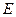
作
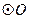
的切線交
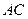
于點(diǎn)
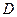
,試判斷
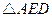
的形狀,并說明理由.
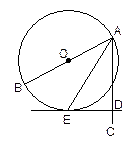
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
已知點(diǎn)C在圓O的直徑BE的延長線上,CA與圓O相切于點(diǎn)A,∠ACB的平分線分別交AB,AE于點(diǎn)D,F(xiàn),則∠ADF=
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
長為
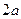
的線段
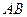
的兩個(gè)端點(diǎn)
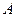
和
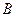
分別在
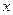
軸和
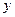
軸上滑動(dòng),求線段
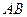
的中點(diǎn)的軌跡方程.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
已知兩圓
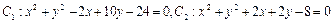
,則以兩圓公共弦為直徑的圓的方程是
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
(幾何證明選講)如圖,點(diǎn)
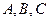
是圓
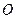
上的點(diǎn),且
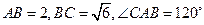
,則
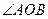
對(duì)應(yīng)的劣弧長為
.
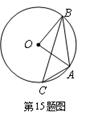
查看答案和解析>>

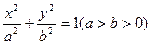 的離心率為
的離心率為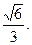
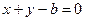 的距離為
的距離為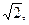 求橢圓的方程;
求橢圓的方程;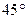 的直線
的直線 和橢圓交于A,B兩點(diǎn).
和橢圓交于A,B兩點(diǎn). ,求b的值;
,求b的值;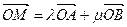 ,求實(shí)數(shù)
,求實(shí)數(shù)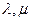 滿足的關(guān)系式.
滿足的關(guān)系式.