
設各項為正數的數列 的前
的前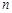 和為
和為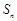 ,且
,且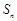 滿足:
滿足: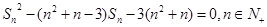 .等比數列
.等比數列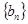 滿足:
滿足: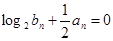 .
.
(Ⅰ)求數列 ,
,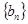 的通項公式;
的通項公式;
(Ⅱ)設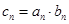 ,求數列
,求數列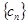 的前
的前 項的和
項的和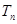 ;
;
(Ⅲ)證明:對一切正整數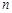 ,有
,有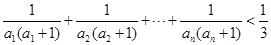 .
.
(1)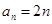 ,
, ;(2)
;(2)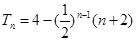 ;(3)證明略.
;(3)證明略.
解析試題分析:(1)給出 與
與 的關系,求
的關系,求 ,常用思路:一是利用
,常用思路:一是利用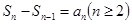 轉化為
轉化為 的遞推關系,再求其通項公式;二是轉化為
的遞推關系,再求其通項公式;二是轉化為 的遞推關系,先求出
的遞推關系,先求出 與
與 的關系,再求
的關系,再求 ;由
;由 推
推 時,別漏掉
時,別漏掉 這種情況,大部分學生好遺忘;(2)一般地,如果數列
這種情況,大部分學生好遺忘;(2)一般地,如果數列 是等差數列,
是等差數列,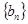 是等比數列,求數列
是等比數列,求數列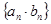 的前
的前 項的和1時,可采用錯位相減法求和,一般是和式兩邊同乘以等比數列
項的和1時,可采用錯位相減法求和,一般是和式兩邊同乘以等比數列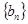 的公比,然后做差求解;(3)利用不等式放縮時掌握好規律,怎樣從條件證明出結論.
的公比,然后做差求解;(3)利用不等式放縮時掌握好規律,怎樣從條件證明出結論.
試題解析:當 時,
時, 即
即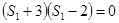 ,又
,又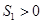 ,
,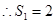 ,即
,即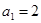
當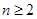 時,
時,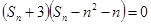 ,又
,又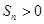 ,
,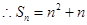
當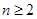 時,
時,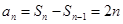
又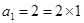
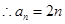
由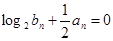 ,得
,得

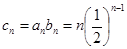
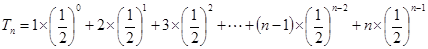
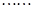 (1)
(1)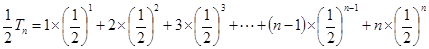
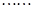 (2)
(2) 得
得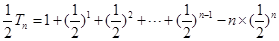
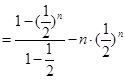
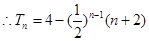 .............................................9分
.............................................9分
(Ⅲ)當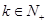 時
時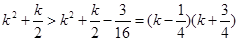
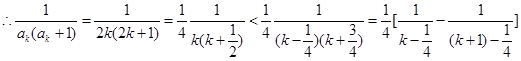
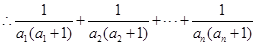
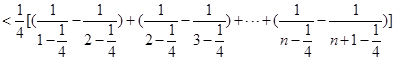
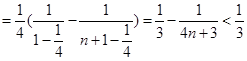 .....................14分
.....................14分
考點:(1)求數列的通項公式;(2)錯位相減求數列的和;(3)證明恒成立的問題.


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com