
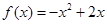 .
.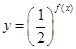 的最小值;
的最小值;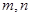 ,當
,當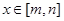 時,
時,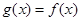 ,且
,且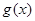 的值域為
的值域為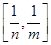 ?若存在,求出所有的
?若存在,求出所有的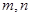 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.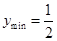 ;(2)
;(2)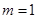 ,
,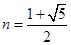 .
.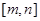 與二次函數
與二次函數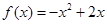 的定對稱軸
的定對稱軸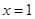 進行比較,自然就會分出它們有三種相對位置關系,即對稱軸
進行比較,自然就會分出它們有三種相對位置關系,即對稱軸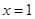 分別在區間
分別在區間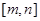 的左、中、右,故討論分三種情形,當然討論必須遵守不重不漏的原則,因此我們還必須關注細節,如區間的端點等,學會討論重要,學會回避討論更重要,它對化繁為簡的能力要求非常高,這里的解法一是分類討論的,而解法二就回避了討論,解得很簡潔,用心體會一下.
的左、中、右,故討論分三種情形,當然討論必須遵守不重不漏的原則,因此我們還必須關注細節,如區間的端點等,學會討論重要,學會回避討論更重要,它對化繁為簡的能力要求非常高,這里的解法一是分類討論的,而解法二就回避了討論,解得很簡潔,用心體會一下.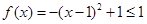 ,令
,令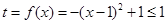
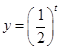 為
為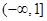 上減函數,因此,則當
上減函數,因此,則當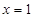 時,
時,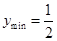 4分
4分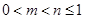 時,
時,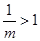
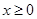 時,
時,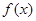 的最大值為
的最大值為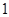 ,故此時不可能使
,故此時不可能使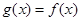 ,且
,且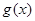 的值域為
的值域為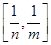 .7分
.7分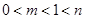 時,
時,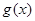 最大值為
最大值為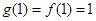 ,即
,即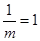 ,
,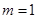 與
與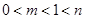 矛盾,故此時不可能. 10分
矛盾,故此時不可能. 10分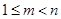 時,
時,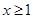 ,
,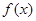 為減函數,則
為減函數,則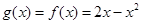
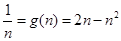 ,即
,即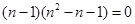 ,
,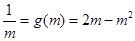
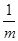 ,即
,即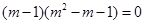
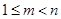 ,∴
,∴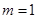 ,
,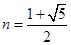 13分
13分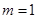 ,
,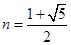 . 14分
. 14分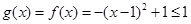 ,
,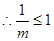 ,即
,即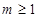 ,即
,即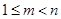 ,
,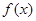 為
為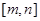 減函數,
減函數,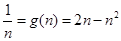 ,即
,即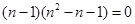 ,
,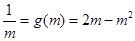
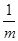 ,即
,即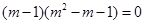
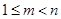 ,∴
,∴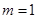 ,
,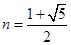 14分
14分

科目:高中數學 來源:不詳 題型:解答題
 )的圍墻,且要求中間用圍墻
)的圍墻,且要求中間用圍墻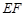 隔開,使得
隔開,使得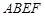 為矩形,
為矩形,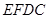 為正方形,設
為正方形,設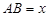 米,已知圍墻(包括
米,已知圍墻(包括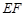 )的修建費用均為800元每米,設圍墻(包括
)的修建費用均為800元每米,設圍墻(包括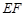 )的修建總費用為
)的修建總費用為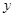 元。
元。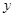 關于
關于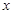 的函數解析式;
的函數解析式;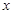 為何值時,設圍墻(包括
為何值時,設圍墻(包括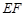 )的的修建總費用
)的的修建總費用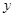 最小?并求出
最小?并求出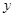 的最小值。
的最小值。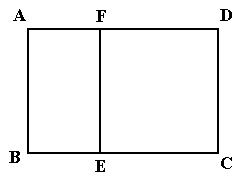
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
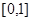 的函數
的函數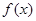 同時滿足以下三個條件:
同時滿足以下三個條件: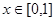 ,總有
,總有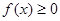 ;
;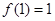 ;
; 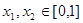 ,且
,且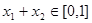 時,
時,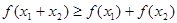 成立.
成立.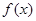 為“友誼函數”,求
為“友誼函數”,求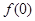 的值;
的值;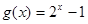 在區間
在區間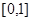 上是否為“友誼函數”?請給出理由;
上是否為“友誼函數”?請給出理由;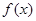 為“友誼函數”,假定存在
為“友誼函數”,假定存在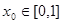 ,使得
,使得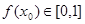 ,且
,且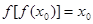 ,求證:
,求證: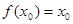 .
.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.?x∈R,aex+x>0 | B.?x∈R,aex+x≥0 |
| C.?x∈R,aex+x≥0 | D.?x∈R,aex+x>0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com