
一盒中裝有9張各寫有一個數字的卡片,其中4張卡片上的數字是1,3張卡片上的數字是2,2張卡片上的數字是3,從盒中任取3張卡片.
(1)求所取3張卡片上的數字完全相同的概率;
(2)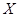 表示所取3張卡片上的數字的中位數,求
表示所取3張卡片上的數字的中位數,求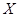 的分布列與數學期望.
的分布列與數學期望.
(注:若三個數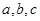 滿足
滿足 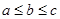 ,則稱
,則稱 為這三個數的中位數).
為這三個數的中位數).
(1)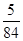 (2)詳見解析.
(2)詳見解析.
解析試題分析:(1)從9張卡片中任取3張,有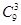 和不同的結果,其中,3張卡片上的數字完全相同的有
和不同的結果,其中,3張卡片上的數字完全相同的有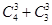 ,由于是任取的,所以每個結果出現的可能性是相等的,故可根據古典概型的概率公式求得概率;
,由于是任取的,所以每個結果出現的可能性是相等的,故可根據古典概型的概率公式求得概率;
(2)由題設隨機變量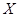 的所有可能取值有1,2,3;
的所有可能取值有1,2,3;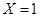 表示抽出的三第卡片上的三個數字可以是
表示抽出的三第卡片上的三個數字可以是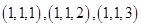
 表示抽出的三第卡片上的三個數字可以是
表示抽出的三第卡片上的三個數字可以是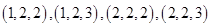
 表示抽出的三第卡片上的三個數字可以是
表示抽出的三第卡片上的三個數字可以是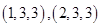
于是可用古典概型的概率公式求出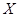 的分布列與數學期望.
的分布列與數學期望.
解:(1)由古典概型中的概率計算公式知所求概率為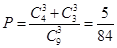
(2)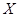 的所有可能值為1,2,3,且
的所有可能值為1,2,3,且 ,
, .
.
故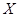 的分布列為
的分布列為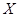
1 2 3 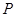
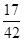
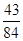
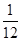
從而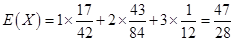
考點:1、組合;2、古典概型;3、離散型隨機變量的分布列與數學期望.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:高中數學 來源: 題型:解答題
為了了解青少年視力情況,某市從高考體檢中隨機抽取16名學生的視力進行調查,經醫生用對數視力表檢查得到每個學生的視力狀況的莖葉圖(以小數點前的一位數字為莖,小數點后的一位數字為葉)如下: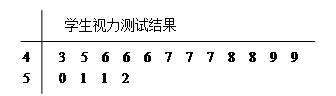
(1)若視力測試結果不低丁5.0,則稱為“好視力”,求校醫從這16人中隨機選取3人,至多有1人是“好視力”的概率;
(2)以這16人的樣本數據來估計該市所有參加高考學生的的總體數據,若從該市參加高考的學生中任選3人,記 表示抽到“好視力”學生的人數,求
表示抽到“好視力”學生的人數,求 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某學校高一年級組建了A、B、C、D四個不同的“研究性學習”小組,要求高一年級學生必須參加,
且只能參加一個小組的活動.假定某班的甲、乙、丙三名同學對這四個小組的選擇是等可能的.
(1)求甲、乙、丙三名同學選擇四個小組的所有選法種數;
(2)求甲、乙、丙三名同學中至少有二人參加同一組活動的概率;
(3)設隨機變量X為甲、乙、丙三名同學參加A小組活動的人數,求X的分布列與數學期望EX.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一紙箱中放有除顏色外,其余完全相同的黑球和白球,其中黑球2個,白球3個.
(1)從中同時摸出兩個球,求兩球顏色恰好相同的概率;
(2)從中摸出一個球,放回后再摸出一個球,求兩球顏色恰好不同的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
隨機觀測生產某種零件的某工廠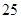 名工人的日加工零件數(單位:件),獲得數據如下:
名工人的日加工零件數(單位:件),獲得數據如下: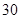 、
、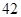 、
、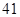 、
、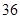 、
、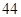 、
、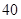 、
、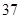 、
、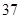 、
、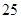 、
、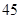 、
、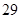 、
、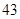 、
、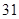 、
、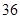 、
、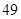 、
、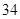 、
、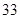 、
、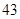 、
、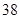 、
、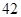 、
、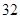 、
、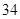 、
、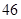 、
、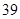 、
、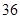 ,根據上述數據得到樣本的頻率分布表如下:
,根據上述數據得到樣本的頻率分布表如下:
| 分組 | 頻數 | 頻率 |
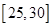 | 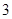 | 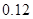 |
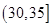 |  |  |
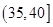 | 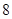 | 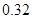 |
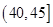 | 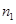 | 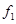 |
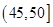 | 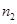 | 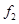 |
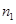 、
、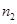 、
、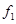 和
和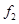 的值;
的值;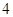 人,至少有
人,至少有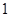 人的日加工零件數落在區間
人的日加工零件數落在區間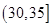 的概率.
的概率.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為喜迎馬年新春佳節,某商場在正月初六進行抽獎促銷活動,當日在該店消費滿500元的顧客可參加抽獎.抽獎箱中有大小完全相同的4個小球,分別標有 “馬”“上”“有”“錢”.顧客從中任意取出1個球,記下上面的字后放回箱中,再從中任取1個球,重復以上操作,最多取4次,并規定若取出“錢”字球,則停止取球.獲獎規則如下:依次取到標有“馬”“上”“有”“錢”字的球為一等獎;不分順序取到標有“馬”“上”“有”“錢”字的球,為二等獎;取到的4個球中有標有“馬”“上”“有”三個字的球為三等獎.
(1)求分別獲得一、二、三等獎的概率;
(2)設摸球次數為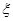 ,求
,求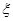 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某公司為招聘新員工設計了一個面試方案:應聘者從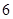 道備選題中一次性隨機抽取
道備選題中一次性隨機抽取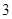 道題,按照題目要求獨立完成.規定:至少正確完成其中
道題,按照題目要求獨立完成.規定:至少正確完成其中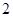 道題的便可通過.已知
道題的便可通過.已知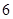 道備選題中應聘者甲有
道備選題中應聘者甲有 道題能正確完成,
道題能正確完成,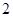 道題不能完成;應聘者乙每題正確完成的概率都是
道題不能完成;應聘者乙每題正確完成的概率都是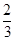 ,且每題正確完成與否互不影響.
,且每題正確完成與否互不影響.
(1)分別求甲、乙兩人正確完成面試題數的分布列,并計算其數學期望;
(2)請分析比較甲、乙兩人誰的面試通過的可能性大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
現有4個人去參加某娛樂活動,該活動有甲、乙兩個游戲可供參加者選擇,為增加趣味性,約定:每個人通過擲一枚質地均勻的骰子決定自己去參加哪個游戲,擲出點數為1或2的人去參加甲游戲,擲出點數大于2的人去參加乙游戲.
(1)求這4個人中恰有2人去參加甲游戲的概率;
(2)求這4個人中去參加甲游戲的人數大于去參加乙游戲的人數的概率;
(3)用X,Y分別表示這4個人中去參加甲、乙游戲的人數,記ξ=|X Y|,求隨機變量ξ的分布列與數學期望Eξ.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某停車場臨時停車按時段收費,收費標準為:每輛汽車一次停車不超過1小時收費6元,超過1小時的部分每小時收費8元(不足1小時的部分按1小時計算).現有甲、乙二人在該停車場臨時停車,兩人停車都不超過4小時.
(1)若甲停車1小時以上且不超過2小時的概率為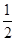 ,停車付費多于14元的概率為
,停車付費多于14元的概率為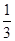 ,求甲臨時停車付費恰為6元的概率;
,求甲臨時停車付費恰為6元的概率;
(2)若每人停車的時間在每個時段的可能性相同,求甲、乙二人停車付費之和為36元的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com