
現有4個人去參加某娛樂活動,該活動有甲、乙兩個游戲可供參加者選擇,為增加趣味性,約定:每個人通過擲一枚質地均勻的骰子決定自己去參加哪個游戲,擲出點數為1或2的人去參加甲游戲,擲出點數大于2的人去參加乙游戲.
(1)求這4個人中恰有2人去參加甲游戲的概率;
(2)求這4個人中去參加甲游戲的人數大于去參加乙游戲的人數的概率;
(3)用X,Y分別表示這4個人中去參加甲、乙游戲的人數,記ξ=|X Y|,求隨機變量ξ的分布列與數學期望Eξ.
(1)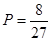 ;(2)
;(2)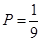 ;(3)分布列詳見解析,
;(3)分布列詳見解析,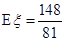 .
.
解析試題分析:本題主要考查隨機事件的概率、獨立重復試驗、離散型隨機變量的分布列和數學期望等基礎知識,考查學生的分析問題解決問題的能力、計算能力.第一問,先通過擲骰子游戲,求出每個人去參加甲游戲和去參加乙游戲的概率,再用獨立重復試驗的計算公式計算4個人中恰有2人去參加甲游戲的概率;第二問,用獨立重復試驗的計算公式計算出去參加甲的人數為3人和4人的概率之和即為所求;第三問,根據前2問的分析,得出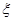 的3個可能取值0,2,4,分別求出概率值,列出分布列,利用
的3個可能取值0,2,4,分別求出概率值,列出分布列,利用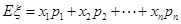 求數學期望.
求數學期望.
依題意,這4個人中,每個人去參加甲游戲的概率為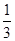 ,去參加乙游戲的概率為
,去參加乙游戲的概率為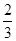 .設“這4個人中恰有i人去參加甲游戲”為事件
.設“這4個人中恰有i人去參加甲游戲”為事件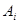 (i=0,1,2,3,4),則
(i=0,1,2,3,4),則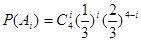
(1)這4個人中恰有2人去參加甲游戲的概率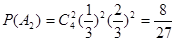 3分
3分
(2)設“這4個人中去參加甲游戲的人數大于去參加乙游戲的人數”為事件B,則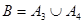 ,
,
由于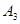 與
與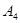 互斥,故
互斥,故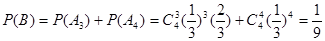
所以,這4個人去參加甲游戲的人數大于去參加乙游戲的人數的概率為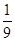 . 7分
. 7分
(3)ξ的所有可能取值為0,2,4.由于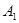 與
與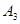 互斥,
互斥,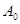 與
與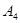 互斥,故
互斥,故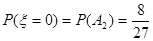 ,
, 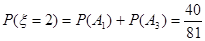
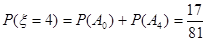 。
。
所以ξ的分布列是ξ 0 2 4 P 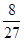
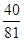
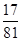
隨機變量ξ的數學期望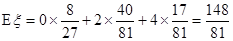 12分
12分
考點:隨機事件的概率、獨立重復試驗、離散型隨機變量的分布列和數學期望.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
一盒中裝有9張各寫有一個數字的卡片,其中4張卡片上的數字是1,3張卡片上的數字是2,2張卡片上的數字是3,從盒中任取3張卡片.
(1)求所取3張卡片上的數字完全相同的概率;
(2)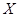 表示所取3張卡片上的數字的中位數,求
表示所取3張卡片上的數字的中位數,求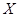 的分布列與數學期望.
的分布列與數學期望.
(注:若三個數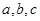 滿足
滿足 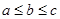 ,則稱
,則稱 為這三個數的中位數).
為這三個數的中位數).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,從參加環保知識競賽的學生中抽出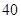 名,將其成績(均為整數)整理后畫出的頻率分布直方圖如下:觀察圖形,回答下列問題:
名,將其成績(均為整數)整理后畫出的頻率分布直方圖如下:觀察圖形,回答下列問題: 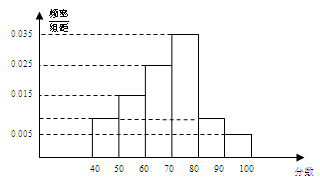
(1)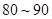 這一組的頻數、頻率分別是多少?
這一組的頻數、頻率分別是多少?
(2)估計這次環保知識競賽成績的平均數、眾數、中位數。(不要求寫過程)
(3) 從成績是80分以上(包括80分)的學生中選兩人,求他們在同一分數段的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一種電腦屏幕保護畫面,只有符號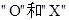 隨機地反復出現,每秒鐘變化一次,每次變化只出現
隨機地反復出現,每秒鐘變化一次,每次變化只出現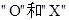 之一,其中出現
之一,其中出現 的概率為p,出現
的概率為p,出現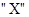 的概率為q,若第k次出現
的概率為q,若第k次出現 ,則記
,則記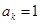 ;出現
;出現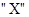 ,則記
,則記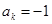 ,令
,令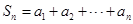 .
.
(1)當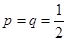 時,求
時,求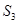 的分布列及數學期望.
的分布列及數學期望.
(2)當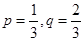 時,求
時,求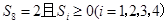 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
從某學校的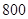 名男生中隨機抽取
名男生中隨機抽取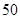 名測量身高,被測學生身高全部介于
名測量身高,被測學生身高全部介于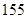 cm和
cm和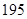 cm之間,將測量結果按如下方式分成八組:第一組[
cm之間,將測量結果按如下方式分成八組:第一組[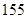 ,
,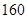 ),第二組[
),第二組[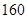 ,
,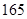 ),…,第八組[
),…,第八組[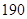 ,
,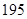 ],右圖是按上述分組方法得到的頻率分布直方圖的一部分,已知第一組與第八組人數相同,第六組的人數為
],右圖是按上述分組方法得到的頻率分布直方圖的一部分,已知第一組與第八組人數相同,第六組的人數為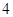 人.
人.
(1)求第七組的頻率并估計該校800名男生中身高在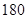 cm以上(含
cm以上(含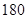 cm)的人數;
cm)的人數;
(2)從第六組和第八組的男生中隨機抽取兩名男生,記他們的身高分別為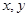 ,事件
,事件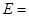 {
{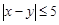 },求
},求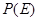 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
下圖是某市3月1日至14日空氣質量指數趨勢圖,空氣質量指數小于1 00表示空氣質量優良,空氣質量指數大于200表示空氣重度污染,某人隨機選擇3月1曰至3月1 3日中某一天到達該市,并停留2天.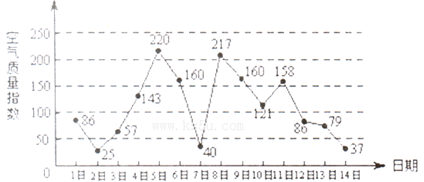
(l)求此人到達當日空氣重度污染的概率;
(2)設X是此人停留期間空氣質量優良的天數,求X的分布列與數學期望。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
現有甲、乙、丙三人參加某電視臺的應聘節目《非你莫屬》,若甲應聘成功的概率為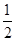 ,乙、丙應聘成功的概率均為
,乙、丙應聘成功的概率均為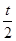 ,(0<t<2),且三個人是否應聘成功是相互獨立的.
,(0<t<2),且三個人是否應聘成功是相互獨立的.
(1)若乙、丙有且只有一個人應聘成功的概率等于甲應聘成功的概率,求t的值;
(2)記應聘成功的人數為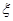 ,若當且僅當為
,若當且僅當為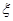 =2時概率最大,求E(
=2時概率最大,求E(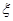 )的取值范圍.
)的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知離散型隨機變量ξ1的概率分布為
| ξ1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P |  |  |  |  |  |  |  |
| ξ2 | 3.7 | 3.8 | 3.9 | 4 | 4.1 | 4.2 | 4.3 |
| P |  |  |  |  |  |  |  |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com