
 .
. 的單調增區(qū)間;
的單調增區(qū)間; ,
, 求b+c的值.
求b+c的值. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
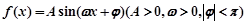 的圖象的一個最高點為
的圖象的一個最高點為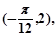 與之相鄰的與
與之相鄰的與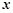 軸的一個交點為
軸的一個交點為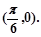
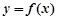 的解析式;
的解析式;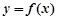 的單調減區(qū)間和函數(shù)圖象的對稱軸方程;
的單調減區(qū)間和函數(shù)圖象的對稱軸方程;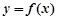 在長度為一個周期區(qū)間上的圖象.
在長度為一個周期區(qū)間上的圖象.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
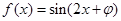 (其中
(其中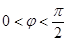 ),滿足
),滿足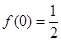 .
.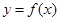 的最小正周期
的最小正周期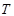 及
及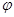 的值;
的值;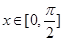 時,求函數(shù)
時,求函數(shù)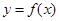 的最小值,并且求使函數(shù)取得最小值的
的最小值,并且求使函數(shù)取得最小值的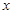 的值.
的值.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 cos 4x.
cos 4x. ,且f(α)=
,且f(α)= ,求α的值.
,求α的值.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
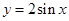 的圖象先向右平移
的圖象先向右平移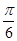 個單位,再將得到的圖象上各點的橫坐標變?yōu)樵瓉淼?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824033500734338.png" style="vertical-align:middle;" />倍(縱坐標不變),得到函數(shù)
個單位,再將得到的圖象上各點的橫坐標變?yōu)樵瓉淼?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824033500734338.png" style="vertical-align:middle;" />倍(縱坐標不變),得到函數(shù)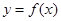 的圖象,若
的圖象,若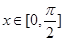 ,則函數(shù)
,則函數(shù)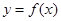 的值域為 .
的值域為 .查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com