
若正項數列 滿足條件:存在正整數
滿足條件:存在正整數 ,使得
,使得 對一切
對一切 都成立,則稱數列
都成立,則稱數列 為
為 級等比數列.
級等比數列.
(1)已知數列 為2級等比數列,且前四項分別為
為2級等比數列,且前四項分別為 ,求
,求 的值;
的值;
(2)若 為常數),且
為常數),且 是
是 級等比數列,求
級等比數列,求 所有可能值的集合,并求
所有可能值的集合,并求 取最小正值時數列
取最小正值時數列 的前
的前 項和
項和 ;
;
(3)證明: 為等比數列的充要條件是
為等比數列的充要條件是 既為
既為 級等比數列,
級等比數列, 也為
也為 級等比數列.
級等比數列.
(1)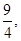 (2)
(2)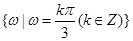 ,0,(3)詳見解析.
,0,(3)詳見解析.
解析試題分析:(1)解新定義數列問題,關鍵從定義出發,建立等量關系.  ,
,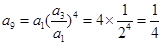 ,
,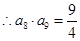 ,(2)本題化簡是關鍵.因為
,(2)本題化簡是關鍵.因為 是
是 級等比數列,所以
級等比數列,所以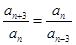
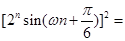
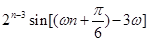
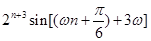

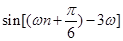
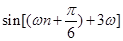
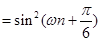
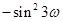
所以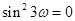 ,
,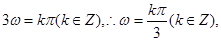
 最小正值等于
最小正值等于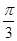 ,此時
,此時
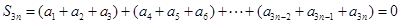 ,(3)充分性就是驗證,易證,關鍵在于證必要性,可從兩者中在交集(共同元素)出發.
,(3)充分性就是驗證,易證,關鍵在于證必要性,可從兩者中在交集(共同元素)出發. 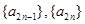 ,
,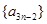 成等比數列, 因此
成等比數列, 因此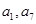 既是
既是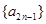 中的項,也是
中的項,也是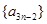 中的項,
中的項, 既是
既是 中的項,也是中
中的項,也是中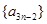 的項,可得它們公比的關系,進而推出三者結構統一,得出等比數列的結論.
的項,可得它們公比的關系,進而推出三者結構統一,得出等比數列的結論.
解(1) (2分)
(2分)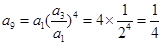
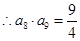 (4分)
(4分)
(2) 是
是 級等比數列,
級等比數列,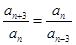
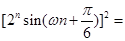
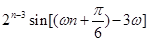
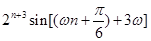 (1分)
(1分)
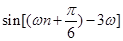
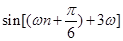
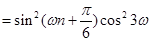
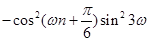
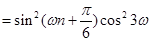
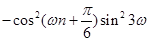
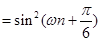
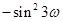
所以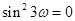 ,
,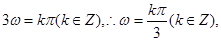
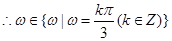 (3分)
(3分) 最小正值等于
最小正值等于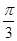 ,此時
,此時
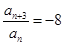 ,
,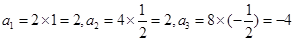 ,
,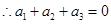
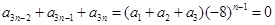 (5分)
(5分)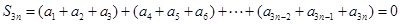 (6分)
(6分)
(3)充分性:若 為等比數列,則
為等比數列,則
對一切 成立,顯然對
成立,顯然對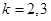 成立。
成立。
所以 既為
既為 級等比數列,
級等比數列, 也為
也為 級等比數列。 (2分)
級等比數列。 (2分)
必要性:若 為
為 級等比數列,
級等比數列,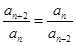 ,則
,則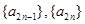 均成等比數列,設等比數列
均成等比數列,設等比數列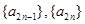 的公比分別為
的公比分別為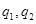 ,
, 為
為

科目:高中數學 來源: 題型:解答題
某種平面分形圖如下圖所示,一級分形圖是由一點出發的三條線段,長度均為1,兩兩夾角為 ;二級分形圖是在一級分形圖的每條線段的末端出發再生成兩條長度為原來
;二級分形圖是在一級分形圖的每條線段的末端出發再生成兩條長度為原來 的線段,且這兩條線段與原線段兩兩夾角為
的線段,且這兩條線段與原線段兩兩夾角為 ;依此規律得到
;依此規律得到 級分形圖.
級分形圖.
(1) 級分形圖中共有 條線段;
級分形圖中共有 條線段;
(2) 級分形圖中所有線段長度之和為 .
級分形圖中所有線段長度之和為 .
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某市為控制大氣PM2.5的濃度,環境部門規定:該市每年的大氣主要污染物排放總量不能超過55萬噸,否則將采取緊急限排措施.已知該市2013年的大氣主要污染物排放總量為40萬噸,通過技術改造和倡導綠色低碳生活等措施,此后每年的原大氣主要污染物排放最比上一年的排放總量減少10%.同時,因為經濟發展和人口增加等因素,每年又新增加大氣主要污染物排放量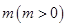 萬噸.
萬噸.
(1)從2014年起,該市每年大氣主要污染物排放總量(萬噸)依次構成數列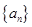 ,求相鄰兩年主要污染物排放總量的關系式;
,求相鄰兩年主要污染物排放總量的關系式;
(2)證明:數列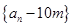 是等比數列;
是等比數列;
(3)若該市始終不需要采取緊急限排措施,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
等比數列{an}中,a1,a2,a3分別是下表第一、二、三行中的某一個數,且a1,a2,a3中的任何兩個數不在下表的同一列.
(1)求數列{an}的通項公式;
(2)若數列{bn}滿足:bn=an+(-1)nlnan,求數列{bn}的前n項和Sn·
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在各項均為正數的等比數列{an}中,已知a2=2a1+3,且3a2,a4,5a3成等差數列.
(1)求數列{an}的通項公式;
(2)設bn=log3an,求數列{anbn}的前n項和Sn.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com