
設函數f(x)=(1+x)2-2ln (1+x).
(1)求函數f(x)的單調區間;
(2)若關于x的方程f(x)=x2+x+a在[0,2]上恰有兩個相異實根,求實數a的取值范圍.
(1)f(x)的遞增區間是(0,+∞),遞減區間是(-1,0).
(2)(2-2ln 2,3-2ln 3].
解析試題分析:解 (1)函數的定義域為(-1,+∞),
因為f(x)=(1+x)2-2ln(1+x),
所以f′(x)=2 =
= ,
,
由f′(x)>0,得x>0;由f′(x)<0,得-1<x<0,
所以,f(x)的遞增區間是(0,+∞),遞減區間是(-1,0).
(2)方程f(x)=x2+x+a,即x-a+1-2ln(1+x)=0,
記g(x)=x-a+1-2ln(1+x)(x>-1),
則g′(x)=1- =
= ,
,
由g′(x)>0,得x>1;
由g′(x)<0,得-1<x<1.
所以g(x)在[0,1]上單調遞減,在[1,2]上單調遞增.
為使f(x)=x2+x+a在[0,2]上恰有兩個相異的實根,
只須g(x)=0在[0,1)和(1,2]上各有一個實根,
于是有 即
即
解得2-2ln 2<a≤3-2ln 3,
故實數a的取值范圍是(2-2ln 2,3-2ln 3].
考點:導數的運用,以及函數與方程
點評:解決的關鍵是根據導數判定函數單調性,以及函數的零點問題,屬于中檔題。


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:解答題
設函數 (1)當
(1)當 時,求
時,求 的最大值;(2)令
的最大值;(2)令 ,(
,( ),其圖象上任意一點
),其圖象上任意一點 處切線的斜率
處切線的斜率 ≤
≤ 恒成立,求實數
恒成立,求實數 的取值范圍;(3)當
的取值范圍;(3)當 ,
, ,方程
,方程 有唯一實數解,求正數
有唯一實數解,求正數 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設 為常數,已知函數
為常數,已知函數 在區間
在區間 上是增函數,
上是增函數,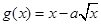 在區間
在區間 上是減函數.
上是減函數.
(1)設 為函數
為函數 的圖像上任意一點,求點
的圖像上任意一點,求點 到直線
到直線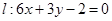 的距離的最小值;
的距離的最小值;
(2)若對任意的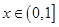 且
且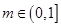 ,
, 恒成立,求實數
恒成立,求實數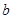 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com