
已知橢圓C的中心在坐標原點,焦點在x軸上,左、右焦點分別為F1,F(xiàn)2,且|F1F2|=2,點P(1,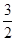 )在橢圓C上.
)在橢圓C上.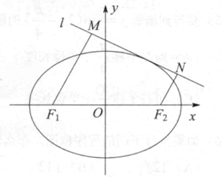
(I)求橢圓C的方程;
(II)如圖,動直線 :
: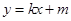 與橢圓C有且僅有一個公共點,點M,N是直線l上的兩點,且
與橢圓C有且僅有一個公共點,點M,N是直線l上的兩點,且 ,
,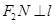 ,四邊形
,四邊形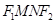 面積S的求最大值.
面積S的求最大值.
(I) ;(II)
;(II) .
.
解析試題分析:(I)設出橢圓的方程,根據(jù)已知條件列方程組,求出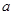 和
和 的值,然后寫出橢圓的標準方程;(II)根據(jù)動直線與橢圓的交點個數(shù),聯(lián)立方程組求的關(guān)系式
的值,然后寫出橢圓的標準方程;(II)根據(jù)動直線與橢圓的交點個數(shù),聯(lián)立方程組求的關(guān)系式 ,再由點到直線的距離公式求得
,再由點到直線的距離公式求得 和
和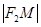 的代數(shù)式,因為四邊形是直角梯形,根據(jù)邊的關(guān)系求得高
的代數(shù)式,因為四邊形是直角梯形,根據(jù)邊的關(guān)系求得高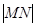 的代數(shù)式,由梯形的面積公式表示出面積
的代數(shù)式,由梯形的面積公式表示出面積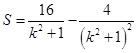 ,利用等量代換
,利用等量代換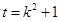 ,化簡
,化簡 的解析式,由函數(shù)的單調(diào)性與導數(shù)的關(guān)系判斷函數(shù)
的解析式,由函數(shù)的單調(diào)性與導數(shù)的關(guān)系判斷函數(shù) 的單調(diào)性,根據(jù)單調(diào)性求最值.
的單調(diào)性,根據(jù)單調(diào)性求最值.
試題解析:(I)設橢圓 的方程為
的方程為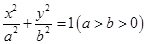 ,
,
由已知可得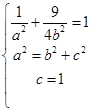 , 3分
, 3分
解得 ,
,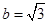 ,
,
∴橢圓 的方程為
的方程為 . 5分
. 5分
(II)由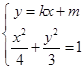 ,得
,得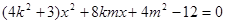 6分
6分
由直線 與橢圓
與橢圓 僅有一個公共點知,
僅有一個公共點知,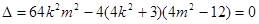 ,
,
化簡得 . 7分
. 7分
由點到直線的距離公式,可設 ,
,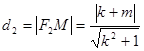 8分
8分
∵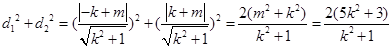 ,
, ,
,
∴ .
.
∴四邊形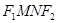 面積
面積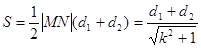 . 10分
. 10分 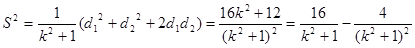
令 ,
, ,
, ,
,
當 時,
時,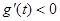 ,∴
,∴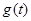 在
在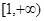 上為減函數(shù),
上為減函數(shù),
∴ ,∴當
,∴當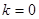 時,
時,
所以四邊形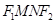 的面積
的面積 的最大值為
的最大值為 . 12分
. 12分
考點:1、橢圓的定義及標準方程;2、點到直線的距離公式;3、梯形的面積公式;4、利用導數(shù)研究函數(shù)的單調(diào)性;5、利用導數(shù)求函數(shù)的最值.


科目:高中數(shù)學 來源: 題型:解答題
已知橢圓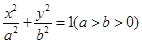 的離心率
的離心率 ,連接橢圓的四個頂點得到的菱形的面積為4.
,連接橢圓的四個頂點得到的菱形的面積為4.
(1)求橢圓的方程;
(2)設直線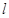 與橢圓相交于不同的兩點A,B。已知點A的坐標為
與橢圓相交于不同的兩點A,B。已知點A的坐標為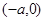 。若
。若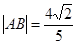 ,求直線
,求直線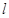 的傾斜角。
的傾斜角。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
設拋物線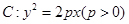 的焦點為
的焦點為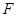 ,準線為
,準線為 ,
,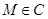 ,以
,以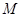 為圓心的圓
為圓心的圓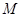 與
與 相切于點
相切于點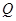 ,
,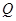 的縱坐標為
的縱坐標為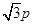 ,
,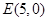 是圓
是圓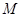 與
與 軸除
軸除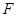 外的另一個交點.
外的另一個交點.
(I)求拋物線 與圓
與圓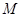 的方程;
的方程;
( II)已知直線 ,
,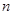 與
與 交于
交于 兩點,
兩點,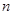 與
與 交于點
交于點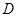 ,且
,且 , 求
, 求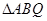 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
如圖已知拋物線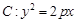 的焦點坐標為
的焦點坐標為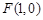 ,過
,過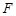 的直線交拋物線
的直線交拋物線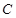 于
于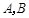 兩點,直線
兩點,直線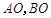 分別與直線
分別與直線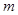 :
: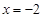 相交于
相交于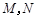 兩點.
兩點.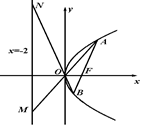
(1)求拋物線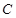 的方程;
的方程;
(2)證明△ABO與△MNO的面積之比為定值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知橢圓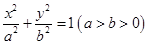 的離心率為
的離心率為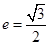 ,直線
,直線 與以原點為圓心、橢圓
與以原點為圓心、橢圓 的短半軸長為半徑的圓
的短半軸長為半徑的圓 相切.
相切.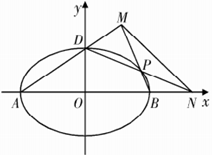
(1)求橢圓 的方程;
的方程;
(2)如圖,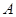 、
、 、
、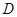 是橢圓
是橢圓 的頂點,
的頂點, 是橢圓
是橢圓 上除頂點外的任意點,直線
上除頂點外的任意點,直線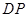 交
交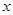 軸于點
軸于點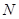 ,直線
,直線 交
交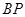 于點
于點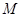 ,設
,設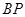 的斜率為
的斜率為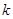 ,
,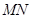 的斜率為
的斜率為 ,求證:
,求證: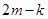 為定值.
為定值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知橢圓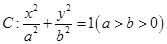 過點
過點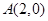 ,離心率為
,離心率為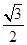 .
.
(Ⅰ)求橢圓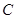 的方程;
的方程;
(Ⅱ)過點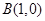 且斜率為
且斜率為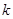 (
(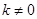 )的直線
)的直線 與橢圓
與橢圓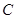 相交于
相交于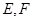 兩點,直線
兩點,直線 、
、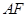 分別交直線
分別交直線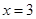 于
于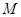 、
、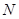 兩點,線段
兩點,線段 的中點為
的中點為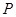 .記直線
.記直線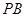 的斜率為
的斜率為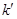 ,求證:
,求證: 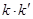 為定值.
為定值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知橢圓 :
:
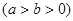 ,
,
(1)若橢圓的長軸長為4,離心率為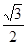 ,求橢圓的標準方程;
,求橢圓的標準方程;
(2)在(1)的條件下,設過定點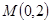 的直線
的直線 與橢圓
與橢圓 交于不同的兩點
交于不同的兩點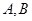 ,且
,且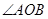 為銳角(
為銳角( 為坐標原點),求直線
為坐標原點),求直線 的斜率
的斜率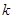 的取值范圍;
的取值范圍;
(3)過原點 任意作兩條互相垂直的直線與橢圓
任意作兩條互相垂直的直線與橢圓 :
:
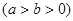 相交于
相交于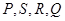 四點,設原點
四點,設原點 到四邊形
到四邊形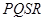 的一邊距離為
的一邊距離為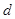 ,試求
,試求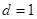 時
時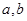 滿足的條件.
滿足的條件.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知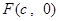 是橢圓
是橢圓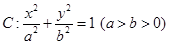 的右焦點,圓
的右焦點,圓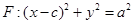 與
與 軸交于
軸交于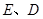 兩點,
兩點,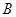 是橢圓
是橢圓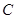 與圓
與圓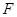 的一個交點,且
的一個交點,且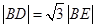
(Ⅰ)求橢圓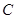 的離心率;
的離心率;
(Ⅱ)過點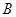 與圓
與圓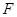 相切的直線
相切的直線 與
與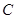 的另一交點為
的另一交點為 ,且
,且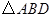 的面積為
的面積為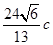 ,求橢圓
,求橢圓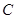 的方程
的方程
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知橢圓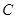 的中心在坐標原點,右準線為
的中心在坐標原點,右準線為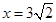 ,離心率為
,離心率為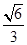 .若直線
.若直線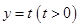 與橢圓
與橢圓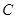 交于不同的兩點
交于不同的兩點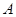 、
、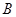 ,以線段
,以線段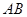 為直徑作圓
為直徑作圓 .
.
(1)求橢圓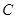 的標準方程;
的標準方程;
(2)若圓 與
與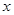 軸相切,求圓
軸相切,求圓 被直線
被直線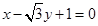 截得的線段長.
截得的線段長.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com