已知
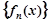
滿足:
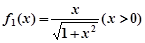
,
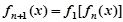
(1)求

;
(2)猜想
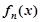
的表達式,并用數(shù)學歸納法證明你的結論
解:⑴
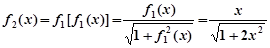
。。。。。。。1分
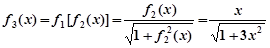
。。。。。。。2分
⑵猜想:
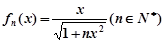
。。。。。。。4分
下面用數(shù)學歸納法證明:
① 當n=1時,
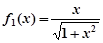
,顯然成立 。。。。。。。。5分
②假設當
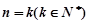
時 ,猜想成立,即
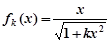
。。。。。。。6分
則當

時,
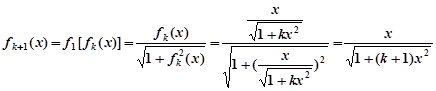
即對
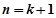
時,猜想也成立。
結合①②可知:猜想
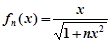
對一切

都成立 。。。。。。。。8分
本試題主要是考查了函數(shù)解析式的求解以及運用數(shù)學歸納法來證明猜想的運用。
(1)因為
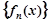
滿足:
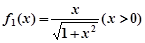
,則可以對n令值,得到

(2)根據(jù)上一問的結論,歸納猜想可知,
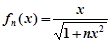
,然后運用數(shù)學歸納法分為兩步驟來鄭敏得到結論。
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:填空題
若
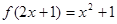
,則
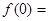
_______________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
將進貨價為8元的商品按每件10元售出,每天可銷售200件;若每件的售價漲0.5元,其銷售量減少10件,問將售價定為多少時,才能使所賺利潤最大?并求出這個最大利潤.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設
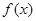
為定義在R上的奇函數(shù),當
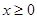
時,
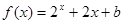
(
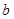
為常數(shù)),則
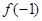
=( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
設函數(shù)
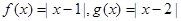
.
(Ⅰ)解不等式
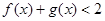
;
(Ⅱ)對于實數(shù)
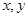
,若

,求證
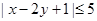
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知集合
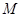
是滿足下列性質函數(shù)的
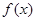
的全體,在定義域
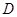
內存在
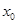
,使得
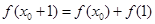
成立。(1)函數(shù)
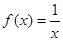
,
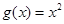
是否屬于集合
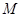
?分別說明理由。(2)若函數(shù)
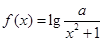
屬于集合
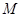
,求實數(shù)
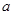
的取值范圍。
查看答案和解析>>

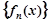 滿足:
滿足: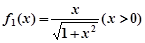 ,
,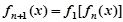
 ;
;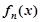 的表達式,并用數(shù)學歸納法證明你的結論
的表達式,并用數(shù)學歸納法證明你的結論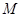 是滿足下列性質函數(shù)的
是滿足下列性質函數(shù)的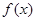 的全體,在定義域
的全體,在定義域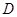 內存在
內存在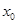 ,使得
,使得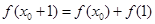 成立。(1)函數(shù)
成立。(1)函數(shù)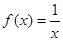 ,
,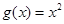 是否屬于集合
是否屬于集合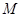 ?分別說明理由。(2)若函數(shù)
?分別說明理由。(2)若函數(shù)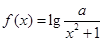 屬于集合
屬于集合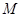 ,求實數(shù)
,求實數(shù)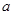 的取值范圍。
的取值范圍。