|
|
|
在直角坐標系xOy中,以坐標原點為極點,x軸正半軸為極軸建立極坐標系,半圓C的極坐標方程為ρ=2cos , , ∈[0, ∈[0,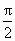 ]. ].
(Ⅰ)求C的參數方程;
(Ⅱ)設點D在C上,C在D處的切線與直線l: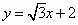 垂直,根據(Ⅰ)中你得到的參數方程,確定D的坐標. 垂直,根據(Ⅰ)中你得到的參數方程,確定D的坐標.
|
|
|
練習冊系列答案
相關習題
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
如圖,四凌錐p-ABCD中,底面ABCD為矩形,PA上面ABCD,E為PD的點.
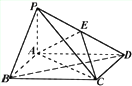
(Ⅰ)證明:PP∥平面AEC;
(Ⅱ)設置AP=1,AD=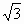 ,三凌P-ABD的體積V= ,三凌P-ABD的體積V=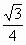 ,求A到平面PBC的距離. ,求A到平面PBC的距離.
|
|
|
查看答案和解析>>
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分別是A1B1,A1C1的中點,BC=CA=CC1,則BM與AN所成角的余弦值為
|
| [ ] |
A. |
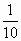
|
B. |
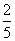
|
C. |
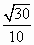
|
D. |
|
|
|
查看答案和解析>>
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
如圖,四棱錐p-ABCD中,底面ABCD為矩形,PA⊥平面ABCD,E為PD的中點.
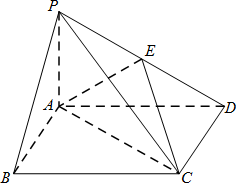
(Ⅰ)證明:PB∥平面AEC;
(Ⅱ)設二面角D-AE-C為60°,AP=1,AD=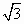 ,求三棱錐E-ACD的體積. ,求三棱錐E-ACD的體積.
|
|
|
查看答案和解析>>
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
若向量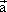 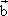 滿足:| 滿足:|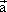 |=1,( |=1,(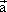 + +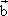 )⊥ )⊥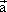 (2 (2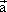 + +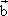 )⊥ )⊥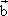 ,則| ,則|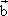 |= |=
|
| [ ] |
A. |
2
|
B. |
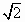
|
C. |
1
|
D. |
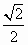
|
|
|
查看答案和解析>>
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
已知二面角α-l-β為60°,AB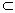 α,AB⊥l,A為垂足,CD α,AB⊥l,A為垂足,CD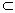 β,C∈l,∠ACD=135°,則異面直線AB與CD所成角的余弦值為 β,C∈l,∠ACD=135°,則異面直線AB與CD所成角的余弦值為
|
| [ ] |
A. |
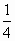
|
B. |
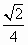
|
C. |
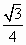
|
D. |
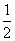
|
|
|
查看答案和解析>>
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
為了了解1000名學生的學習情況,采用系統抽樣的方法,從中抽取容量為40的樣本,則分段的間隔為
|
| [ ] |
A. |
50
|
B. |
40
|
C. |
25
|
D. |
20
|
|
|
查看答案和解析>>
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
命題“ x∈[0,+∞)x3+x≥0”的否定是 x∈[0,+∞)x3+x≥0”的否定是
|
| [ ] |
A. |
 x∈(0,∞)x3+x<0 x∈(0,∞)x3+x<0
|
B. |
 x∈(-∞,0)x3+x≥0 x∈(-∞,0)x3+x≥0
|
C. |
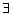 x0∈[0,+∞)x x0∈[0,+∞)x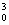 +x0≤0 +x0≤0
|
D. |
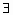 x0∈[0,+∞)x x0∈[0,+∞)x +x0≥0 +x0≥0
|
|
|
查看答案和解析>>
