
已知四棱錐PABCD的底面ABCD是邊長為2的正方形,PD⊥底面ABCD,E,F分別為棱BC,AD的中點(diǎn).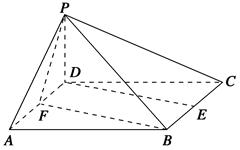
(1)求證:DE∥平面PFB;
(2)已知二面角PBFC的余弦值為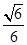 ,求四棱錐PABCD的體積.
,求四棱錐PABCD的體積.
 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在四邊形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2 ,AD=2,求四邊形ABCD繞AD旋轉(zhuǎn)一周所成幾何體的表面積及體積.
,AD=2,求四邊形ABCD繞AD旋轉(zhuǎn)一周所成幾何體的表面積及體積.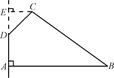
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在邊長為4的菱形ABCD中,∠DAB=60°.點(diǎn)E、F分別在邊CD、CB上,點(diǎn)E與點(diǎn)C、D不重合,EF⊥AC,EF∩AC=O.沿EF將△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED.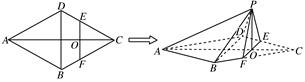
(1)求證:BD⊥平面POA;
(2)記三棱錐P-ABD的體積為V1,四棱錐P-BDEF的體積為V2,求當(dāng)PB取得最小值時(shí)V1∶V2的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,E是以AB為直徑的半圓上異于點(diǎn)A、B的點(diǎn),矩形ABCD所在的平面垂直于該半圓所在的平面,且AB=2AD=2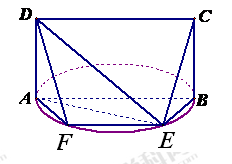
(1)求證: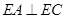
(2)設(shè)平面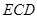 與半圓弧的另一個(gè)交點(diǎn)為
與半圓弧的另一個(gè)交點(diǎn)為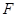
①試證: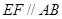
②若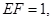 求三棱錐
求三棱錐 的體積
的體積
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在三棱柱ABC-A1B1C1中,C1C⊥底面ABC,AC=BC=CC1=2,AC⊥BC,點(diǎn)D是AB的中點(diǎn).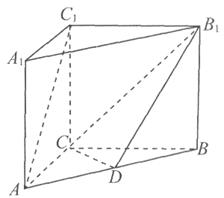
(1)求證:AC1∥平面CDB1;
(2)求四面體B1C1CD的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在四棱錐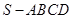 中,底面
中,底面 是正方形,
是正方形,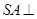 底面
底面 ,
, ,點(diǎn)
,點(diǎn) 是
是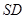 的中點(diǎn),
的中點(diǎn),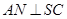 ,交
,交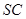 于點(diǎn)
于點(diǎn)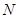 .
.
(1)求證:平面 平面
平面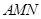 ;
;
(2)求三棱錐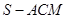 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
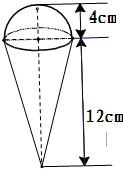
如圖,一個(gè)圓錐形的空杯子上面放著一個(gè)半球形的冰淇淋,如果冰淇淋融化了并流入杯中,會(huì)溢出杯子嗎?請(qǐng)用你的計(jì)算數(shù)據(jù)說明理由。(冰、水的體積差異忽略不計(jì))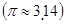
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在邊長為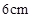 的正方形ABCD中,E、F分別為BC、CD的中點(diǎn),M、N分別為AB、CF的中點(diǎn),現(xiàn)沿AE、AF、EF折疊,使B、C、D三點(diǎn)重合于B,構(gòu)成一個(gè)三棱錐(如圖所示).
的正方形ABCD中,E、F分別為BC、CD的中點(diǎn),M、N分別為AB、CF的中點(diǎn),現(xiàn)沿AE、AF、EF折疊,使B、C、D三點(diǎn)重合于B,構(gòu)成一個(gè)三棱錐(如圖所示).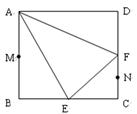
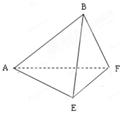
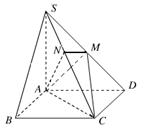
(Ⅰ)在三棱錐上標(biāo)注出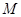 、
、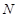 點(diǎn),并判別MN與平面AEF的位置關(guān)系,并給出證明;
點(diǎn),并判別MN與平面AEF的位置關(guān)系,并給出證明;
(Ⅱ)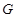 是線段
是線段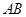 上一點(diǎn),且
上一點(diǎn),且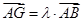 ,問是否存在點(diǎn)
,問是否存在點(diǎn)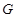 使得
使得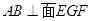 ,若存在,求出
,若存在,求出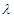 的值;若不存在,請(qǐng)說明理由;
的值;若不存在,請(qǐng)說明理由;
(Ⅲ)求多面體E-AFNM的體積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com