【答案】
分析:根據(jù)題意,算出圓C
2關(guān)于直線(xiàn)l對(duì)稱(chēng)的圓C'方程為(x-5)
2+(y+2)
2=1.當(dāng)點(diǎn)P位于線(xiàn)段C
1C'上時(shí),線(xiàn)段AB'長(zhǎng)是圓C
1與圓C'上兩個(gè)動(dòng)點(diǎn)之間的距離最小值,由此結(jié)合對(duì)稱(chēng)的知識(shí)與兩點(diǎn)間的距離公式加以計(jì)算,即可得出|PA|+|PB|的最小值.
解答:解:設(shè)圓C'是圓C
2:x
2+(y-3)
2=1關(guān)于直線(xiàn)l對(duì)稱(chēng)的圓
可得C'(5,-2),圓C'方程為(x-5)
2+(y+2)
2=1

可得當(dāng)點(diǎn)P位于線(xiàn)段C
1C'上時(shí),線(xiàn)段AB'長(zhǎng)是圓C
1與圓C'上兩個(gè)動(dòng)點(diǎn)之間的距離最小值
B'關(guān)于直線(xiàn)l對(duì)稱(chēng)的點(diǎn)在圓C
2上,由平幾知識(shí)得當(dāng)圓C
2上的
動(dòng)點(diǎn)B與該點(diǎn)重合時(shí),|PA|+|PB|達(dá)到最小值
∵|C
1C'|=

=
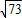
,
可得|AB'|=|C
1C'|-r
1-r
2=

因此,|PA|+|PB|的最小值等于|AB'|=

故答案為:
 點(diǎn)評(píng):
點(diǎn)評(píng):本題給出直線(xiàn)l與兩個(gè)定圓,求圓上兩個(gè)點(diǎn)A、B與直線(xiàn)l上動(dòng)點(diǎn)P的距離之和的最小值,著重考查了直線(xiàn)的方程、圓的方程和直線(xiàn)與圓的位置關(guān)系等知識(shí),屬于中檔題.


 =
=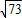 ,
,




 陽(yáng)光課堂課時(shí)作業(yè)系列答案
陽(yáng)光課堂課時(shí)作業(yè)系列答案
 (2011•武昌區(qū)模擬)如圖,已知點(diǎn)P是圓上C:x2+(y-2
(2011•武昌區(qū)模擬)如圖,已知點(diǎn)P是圓上C:x2+(y-2