
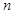 及天數如下表:
及天數如下表:售出個數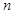 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天數 | 3 | 3 | 3 | 6 | 9 | 6 |
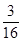 ;(3)分布列為
;(3)分布列為利潤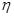 | 80 | 95 | 110 | 125 | 140 |
概率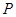 | 0.1 | 0.1 | 0.1 | 0.2 | 0.5 |
 ,再由小王某天售出該現烤面包恰14個和恰15個這兩個事件是互斥的,所以小王某天售出該現烤面包超過13個的概率就等于上述兩個概率之和為:0.3+0.2=0.5.
,再由小王某天售出該現烤面包恰14個和恰15個這兩個事件是互斥的,所以小王某天售出該現烤面包超過13個的概率就等于上述兩個概率之和為:0.3+0.2=0.5.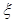 ,由于每天售出的個數要么超過13個,要么不超過13個只有這兩種結果,且兩種結果發生與否互相對立,并且相互獨立,與其它各次試驗結果無關,事件發生與否的概率在每一次獨立試驗中都保持不變各為0.5,所以
,由于每天售出的個數要么超過13個,要么不超過13個只有這兩種結果,且兩種結果發生與否互相對立,并且相互獨立,與其它各次試驗結果無關,事件發生與否的概率在每一次獨立試驗中都保持不變各為0.5,所以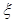 服從參數為5和0.5的二項分布,即
服從參數為5和0.5的二項分布,即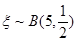 ,從而事件“小王增加訂購量”的概率,即是
,從而事件“小王增加訂購量”的概率,即是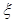 >3的概率,而
>3的概率,而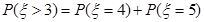 ,再由二項分布的概率公式
,再由二項分布的概率公式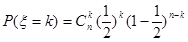 可算得事件“小王增加訂購量”的概率;
可算得事件“小王增加訂購量”的概率; 元,由已知求出
元,由已知求出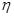 的所有可能取值,并結合題只所給條件可得到
的所有可能取值,并結合題只所給條件可得到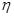 的每一個可能取值的概率,從而求得其分布列,在由數學期望公式:
的每一個可能取值的概率,從而求得其分布列,在由數學期望公式: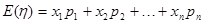 就可求得所獲利潤的數學期望.
就可求得所獲利潤的數學期望.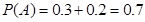 . 2分
. 2分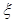 ,
, 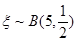 . ..5分
. ..5分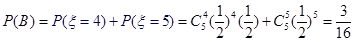 ,
,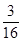 . 8分
. 8分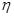 元,則
元,則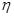 的所有可能取值為80,95,110,125,140. 9分
的所有可能取值為80,95,110,125,140. 9分 利潤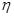 | 80 | 95 | 110 | 125 | 140 |
概率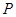 | 0.1 | 0.1 | 0.1 | 0.2 | 0.5 |
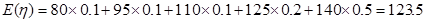


科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
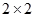 列聯表:
列聯表: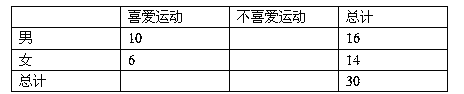
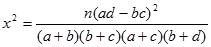 (其中
(其中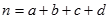 )
)| | 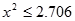 | 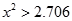 | 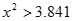 | 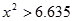 |
| 是否有關聯 | 沒有關聯 | 90% | 95% | 99% |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| | 優秀 | 非優秀 | 總計 |
| 甲班 | 20 | | |
| 乙班 | | 60 | |
| 總計 | | | 210 |
 .
.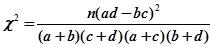 ,其中
,其中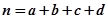 .
.| 參考數據 | 當 ≤2.706時,無充分證據判定變量A,B有關聯,可以認為兩變量無關聯; ≤2.706時,無充分證據判定變量A,B有關聯,可以認為兩變量無關聯; |
當 >2.706時,有90%的把握判定變量A,B有關聯; >2.706時,有90%的把握判定變量A,B有關聯; | |
當 >3.841時,有95%的把握判定變量A,B有關聯; >3.841時,有95%的把握判定變量A,B有關聯; | |
當 >6.635時,有99%的把握判定變量A,B有關聯. >6.635時,有99%的把握判定變量A,B有關聯. |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 患病 | 未患病 | 總計 | |
| 沒服用藥 | 20 | 30 | 50 |
| 服用藥 | x | y | 50 |
| 總計 | M | N | 100 |
| 38 |
| 9 |
| n(ad-bc)2 |
| (a+b)(b+c)(a+c)(b+d) |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 |
| k | 1.323 | 2.072 | 2.706 | 3.845 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.0.48 | B.0.52 | C.0.8 | D.0.92 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com