
動圓M過定點A(- ,0),且與定圓A´:(x-
,0),且與定圓A´:(x- )2+y2=12相切.
)2+y2=12相切.

(1)求動圓圓心M的軌跡C的方程;
(2)過點P(0,2)的直線l與軌跡C交于不同的兩點E、F,求 的取值范圍.
的取值范圍.
(1)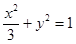 (2)
(2)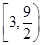
【解析】
試題分析:(1)A´(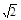 ,0),依題意有|MA´|+
,0),依題意有|MA´|+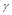 =2
=2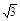
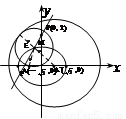
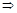 |MA´|+|MA|
|MA´|+|MA|
=2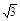 >2
>2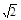 3分
3分
∴點M的軌跡是以A´、A為焦點,2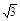 為長軸上的橢圓,∵a=
為長軸上的橢圓,∵a=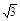 ,c=
,c=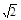 ∴b2=1.因此點M的軌跡方程為
∴b2=1.因此點M的軌跡方程為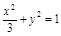 5分
5分
(2) 解:設l的方程為x=k(y-2)代入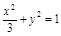 ,消去x得:(k2+3)
y2-4k2y+4k2-3=0
,消去x得:(k2+3)
y2-4k2y+4k2-3=0
由△>0得16k4-(4k2-3)(k2+3)>0 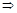 0≤k2<1 7分
0≤k2<1 7分
設E(x1,y1),F(x2,y2),
則y1+y2=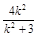 ,y1y2=
,y1y2=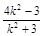
又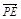 =(x1,y1-2),
=(x1,y1-2),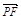 =(x2,y2-2)
=(x2,y2-2)
∴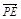 ·
·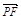 =x1x2+(y1-2)(y2-2)
=x1x2+(y1-2)(y2-2)
=k(y1-2)·k (y2-2) +(y1-2)(y2-2)
=(1+k2)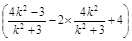
=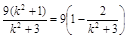 10分
10分
∵0≤k2<1 ∴3≤k2+3<4 ∴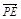 ·
·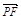 ∈
∈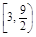 12分
12分
考點:動點的軌跡方程軌跡方程及直線與圓相交的位置關系
點評:求軌跡方程大體步驟:1建立坐標系,設出所求點,2,找到動點滿足的關系,3關系式坐標化整理化簡,4去除不滿足要求的點


科目:高中數學 來源: 題型:
 動圓M過定點A(-
動圓M過定點A(-| 2 |
| 2 |
| PE |
| PF |
查看答案和解析>>
科目:高中數學 來源:2014屆浙江省高二5月教學質量檢測理科數學卷(解析版) 題型:解答題
動圓M過定點A(- ,0),且與定圓A´:(x-
,0),且與定圓A´:(x- )2+y2=12相切.
)2+y2=12相切.
(1)求動圓圓心M的軌跡C的方程;
(2)過點P(0,2)的直線l與軌跡C交于不同的兩點E、F,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 動圓M過定點A(-
動圓M過定點A(- ,0),且與定圓A?:(x-
,0),且與定圓A?:(x- )2+y2=12相切.
)2+y2=12相切.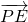 •
• 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數學 來源:2012-2013學年山東省德州市某中學高三(上)12月月考數學試卷(理科)(解析版) 題型:解答題
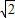 ,0),且與定圓A´:(x-
,0),且與定圓A´:(x-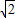 )2+y2=12相切.
)2+y2=12相切.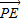 •
•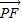 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com