
如圖,漁船甲位于島嶼A的南偏西60°方向的B處,且與島嶼A相距12海里,漁船乙以10海里/時的速度從島嶼A出發沿正北方向航行,若漁船甲同時從B處出發沿北偏東α的方向追趕漁船乙,剛好用2小時追上,此時到達C處.
(1)求漁船甲的速度;
(2)求sinα的值.
(1)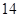 海里/小時;(2)
海里/小時;(2)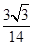 .
.
解析試題分析:(1)首先利用余弦定理求出BC,即可求出漁船甲的速度;
(2)由余弦定理求出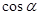 ,再利用同角及泵西求出
,再利用同角及泵西求出 .
.
試題解析:解:(1)依題意, ,
, ,
,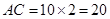 ,
, .
.
在△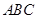 中,由余弦定理,得
中,由余弦定理,得
 .解得
.解得 . 4分
. 4分
所以漁船甲的速度為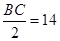 海里/小時.
海里/小時.
答:漁船甲的速度為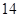 海里/小時. 6分
海里/小時. 6分
(2)在△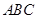 中,因為
中,因為 ,
, ,
, ,
, ,
,
由余弦定理,得 .即
.即 . 9分
. 9分
因為 為銳角,所以
為銳角,所以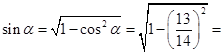
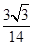 .
.
答: 的值為
的值為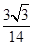 . 12分
. 12分
法二:在△ABC中,因為AB=12(海里),∠BAC=120°,BC=28(海里),∠BCA=α,由正弦定理,得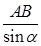 =
= .
.
即sinα=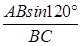 =
= =
=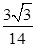 . 11分
. 11分
答: 的值為
的值為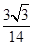 . 12分
. 12分
考點:1.正弦定理和余弦定理;2.同角的基本關系.


 長江作業本同步練習冊系列答案
長江作業本同步練習冊系列答案科目:高中數學 來源: 題型:解答題
已知函數f(x)=(2cos2x-1)sin2x+ cos4x (1)求f(x)的最小正周期及最大值。
cos4x (1)求f(x)的最小正周期及最大值。
(2)設A,B,C為△ABC的三個內角,若cosB=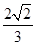 ,f(
,f(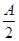 )=-
)=- ,且角A為鈍角,求sinC
,且角A為鈍角,求sinC
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com