
已知函數 .
.
(1)若 在
在 處取得極值,求實數
處取得極值,求實數 的值;
的值;
(2)求函數 的單調區間;
的單調區間;
(3)若 在
在 上沒有零點,求實數
上沒有零點,求實數 的取值范圍.
的取值范圍.
(1) ;(2)單調遞增區間為
;(2)單調遞增區間為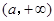 ,單調遞減區間為
,單調遞減區間為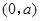 ;(3)
;(3) .
.
解析試題分析:(1)求函數極值分四步,一是求函數定義域
科目:高中數學
來源:
題型:解答題
已知函數
科目:高中數學
來源:
題型:解答題
設函數f(x)=x2-mlnx,g(x)=x2-x+a.
科目:高中數學
來源:
題型:解答題
一個圓柱形圓木的底面半徑為1m,長為10m,將此圓木沿軸所在的平面剖成兩個部分.現要把其中一個部分加工成直四棱柱木梁,長度保持不變,底面為等腰梯形
科目:高中數學
來源:
題型:解答題
已知函數f(x)=(x-a)2(x-b)(a,b∈R,a<b).
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區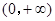 ,二是求函數導數
,二是求函數導數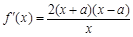 ,三是根據導數為零將定義區間分割,討論導數值正負
,三是根據導數為零將定義區間分割,討論導數值正負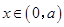 ,
,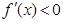 ;
;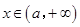 ,
,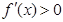 ,,四是根據導數符號變化確定極值點
,,四是根據導數符號變化確定極值點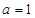 ;(2)利用導數求函數單調性,也是四個步驟.一是求出定義域:,二是求導數,三是分析導數符號變化情況,四是根據導數符號寫出對應單調區間:減區間為
;(2)利用導數求函數單調性,也是四個步驟.一是求出定義域:,二是求導數,三是分析導數符號變化情況,四是根據導數符號寫出對應單調區間:減區間為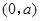 ,增區間
,增區間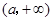 ; (3)
; (3) 在
在 上沒有零點,即
上沒有零點,即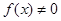 在
在 上恒成立,也就是
上恒成立,也就是 或
或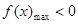 ,又
,又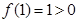 ,只須在區間
,只須在區間 上
上 .以下有兩個思路,一是求最小值,需分類討論,當
.以下有兩個思路,一是求最小值,需分類討論,當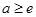 時,
時,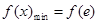 .當
.當 時,
時,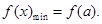 當
當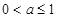 時,
時,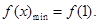 二是變量分離,
二是變量分離,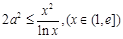 ,只需求函數
,只需求函數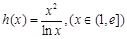 的最小值.
的最小值.
試題解析:解:(1)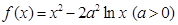 的定義域為
的定義域為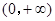 . 1分
. 1分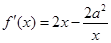
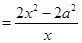
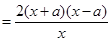 . 2分
. 2分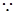
 在
在 處取得極值,
處取得極值,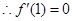 ,解得
,解得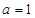 或
或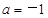 (舍). 3分
(舍). 3分
當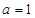 時,
時,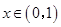 ,
,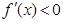 ;
;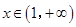 ,
,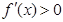 ,
,
所以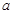 的值為
的值為 . 4分
. 4分
(2)令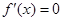 ,解得
,解得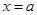 或
或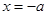 (舍). 5分
(舍). 5分
當 在
在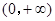 內變化時,
內變化時,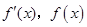 的變化情況如下:
的變化情況如下:
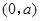

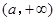



1加1閱讀好卷系列答案
專項復習訓練系列答案
初中語文教與學閱讀系列答案

完形填空與閱讀理解周秘計劃系列答案
英語閱讀理解150篇系列答案
奔騰英語系列答案
標準閱讀系列答案
53English系列答案
考綱強化閱讀系列答案
 ,其中m,a均為實數.
,其中m,a均為實數.
(1)求 的極值;
的極值;
(2)設 ,若對任意的
,若對任意的
 ,
, 恒成立,求
恒成立,求 的最小值;
的最小值;
(3)設 ,若對任意給定的
,若對任意給定的 ,在區間
,在區間 上總存在
上總存在 ,使得
,使得 成立,求
成立,求 的取值范圍.
的取值范圍.
(1)當a=0時,f(x)≥g(x)在(1,+∞),上恒成立,求實數m的取值范圍;
(2)當m=2時,若函數h(x)=f(x)-g(x)在[1,3]上恰有兩個不同的零點,求實數a的取值范圍. (如圖所示,其中O為圓心,
(如圖所示,其中O為圓心, 在半圓上),設
在半圓上),設 ,木梁的體積為V(單位:m3),表面積為S(單位:m2).
,木梁的體積為V(單位:m3),表面積為S(單位:m2).
(1)求V關于θ的函數表達式;
(2)求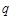 的值,使體積V最大;
的值,使體積V最大;
(3)問當木梁的體積V最大時,其表面積S是否也最大?請說明理由.
(1)當a=1,b=2時,求曲線y=f(x)在點(2,f(2))處的切線方程;
(2)設x1,x2是f(x)的兩個極值點,x3是f(x)的一個零點,且x3≠x1,x3≠x2.證明:存在實數x4,使得x1,x2,x3,x4按某種順序排列后構成等差數列,并求x4.
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號