
如圖1-1-8,在四邊形ABCD中,BC=m,DC=2m,四個(gè)內(nèi)角A、B、C、D之比為3∶7∶4∶10,試求四邊形ABCD的面積

圖1-1-8
思路分析:四邊形的基本構(gòu)成元素是三角形,因而可把該問題轉(zhuǎn)化為求三角形面積,首先可根據(jù)四個(gè)內(nèi)角的度數(shù)之比求出四個(gè)內(nèi)角,結(jié)合余弦定理求得邊長,利用三角形面積公式S=![]() absinC求解.
absinC求解.
解:由題意知,設(shè)四個(gè)內(nèi)角A、B、C、D的大小依次為3x、7x、4x、10x,則3x+7x+4x+10x=360°.
∴x=15°,即A=45°,B=105°,C=60°,D=150°.
在△BCD中,由余弦定理,得
BD2=BC2+DC2-2BC·DC·cosC=m2+(2m)2-2×m×2m×cos60°=3m2.
∴BD=3m.
∴S△BCD=![]() DC·BC·sinC=
DC·BC·sinC=![]() ×m×2m×
×m×2m×![]() =
=![]() m2.
m2.
在△BCD中,BD2+BC2=DC2,∴∠DBC=90°.∴∠BDC=30°.
在△BAD中,由正弦定理,得
AB=![]() =
=![]() =
=![]() m.
m.
又∠ABD=105°-90°=15°,
∴S△ABD=![]() AB·BD·sin15°=
AB·BD·sin15°=![]() ×
×![]() m×
m×![]() m×
m×![]() =
=![]() m2.
m2.
∴S四邊形ABCD=S△BCD+S△ABD=![]() m2+
m2+![]() m2=
m2=![]() m2.
m2.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
 如圖莖葉圖記錄了甲、乙兩組四名同學(xué)的植樹棵數(shù),乙組記錄中有一個(gè)數(shù)據(jù)模糊,無法確認(rèn),在圖中以X表示.
如圖莖葉圖記錄了甲、乙兩組四名同學(xué)的植樹棵數(shù),乙組記錄中有一個(gè)數(shù)據(jù)模糊,無法確認(rèn),在圖中以X表示.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
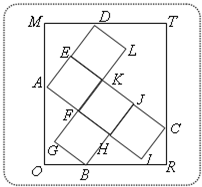 如圖,已知矩形ORTM內(nèi)有5個(gè)全等的小正方形,其中頂點(diǎn)A、B、C、D在矩形ORTM的四條邊上.
如圖,已知矩形ORTM內(nèi)有5個(gè)全等的小正方形,其中頂點(diǎn)A、B、C、D在矩形ORTM的四條邊上.| BD |
| AE |
| AF |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年上海市徐匯區(qū)高三上學(xué)期期末考試?yán)砜茢?shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分14分) 本題共有2個(gè)小題,第1小題滿分6分,第2小題滿分8分.
(理)某種型號(hào)汽車四個(gè)輪胎半徑相同,均為 ,同側(cè)前后兩輪胎之間的距離(指輪胎中心之間距離)為
,同側(cè)前后兩輪胎之間的距離(指輪胎中心之間距離)為 (假定四個(gè)輪胎中心構(gòu)成一個(gè)矩形). 當(dāng)該型號(hào)汽車開上一段上坡路
(假定四個(gè)輪胎中心構(gòu)成一個(gè)矩形). 當(dāng)該型號(hào)汽車開上一段上坡路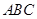 (如圖(1)所示,其中
(如圖(1)所示,其中 (
(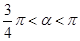 )),且前輪
)),且前輪 已在
已在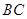 段上時(shí),后輪中心在
段上時(shí),后輪中心在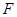 位置;若前輪中心到達(dá)
位置;若前輪中心到達(dá)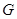 處時(shí),后輪中心在
處時(shí),后輪中心在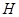 處(假定該汽車能順利駛上該上坡路). 設(shè)前輪中心在
處(假定該汽車能順利駛上該上坡路). 設(shè)前輪中心在 和
和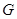 處時(shí)與地面的接觸點(diǎn)分別為
處時(shí)與地面的接觸點(diǎn)分別為 和
和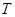 ,且
,且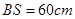 ,
,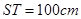 . (其它因素忽略不計(jì))
. (其它因素忽略不計(jì))
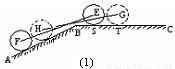
(1)如圖(2)所示,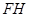 和
和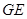 的延長線交于點(diǎn)
的延長線交于點(diǎn) ,
,
求證: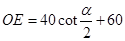 (cm);
(cm);
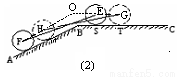
(2)當(dāng)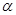 =
=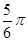 時(shí),后輪中心從
時(shí),后輪中心從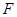 處移動(dòng)到
處移動(dòng)到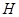 處實(shí)際移動(dòng)了多少厘米? (精確到1cm)
處實(shí)際移動(dòng)了多少厘米? (精確到1cm)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年江西省高二第三次段考數(shù)學(xué)文卷 題型:解答題
如圖1,在直角梯形 中,
中, ,
, ,
, ,
, ,
, 分別是
分別是 的中點(diǎn),現(xiàn)將
的中點(diǎn),現(xiàn)將 沿
沿 折起,使平面
折起,使平面 平面
平面 (如圖2),且所得到的四棱錐
(如圖2),且所得到的四棱錐 的正視圖、側(cè)視圖、俯視圖的面積總和為8.
的正視圖、側(cè)視圖、俯視圖的面積總和為8.
⑴求點(diǎn) 到平面
到平面 的距離;
的距離;
⑵求二面角 的大小的夾角的余弦值;
的大小的夾角的余弦值;
⑶在線段 上確定一點(diǎn)
上確定一點(diǎn) ,使
,使 平面
平面 ,并給出證明過程.
,并給出證明過程.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com