Question

（13分）（2011•重慶）設α∈R，f（x）=cosx（asinx﹣cosx）+cos²（﹣x）滿足，求函數f（x）在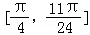上的最大值和最小值．

Answer 1

最大值是： 2  最小值為：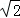

解析試題分析：利用二倍角公式化簡函數f（x），然后，求出a的值，進一步化簡為f（x）=2sin（2x﹣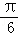），然后根據x的范圍求出2x﹣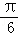，的范圍，利用單調性求出函數的最大值和最小值．
解：f（x）=cosx（asinx﹣cosx）+cos²（﹣x）
=asinxcosx﹣cos²x+sin²x
=
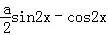
由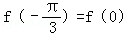得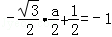
解得a=2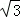
所以f（x）=2sin（2x﹣），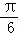
所以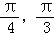x∈[]時2x﹣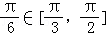，f（x）是增函數，
所以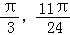x∈[]時2x﹣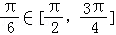，f（x）是減函數，
函數f（x）在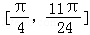上的最大值是：f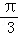（）=2；
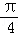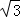又f（）=，f（）=；
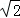所以函數f（x）在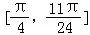上的最小值為：f（）=；
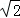點評：本題是中檔題，考查三角函數的化簡，二倍角公式的應用，三角函數的求值，函數的單調性、最值，考查計算能力，常考題型．