
已知向量 ,
, ,且
,且 .
.
求 及
及 ;
;
若 的最小值是
的最小值是 ,求實數
,求實數 的值;
的值;
設 ,若方程
,若方程 在
在 內有兩個不同的解,求實數
內有兩個不同的解,求實數 的取值范圍.
的取值范圍.
(1)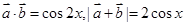 ;(2)
;(2) ;(3)
;(3) 或
或 .
.
解析試題分析:(1)根據已知條件及平面向量的坐標表示與模的坐標表示,
可以得到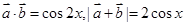 ;
;
由(1)可得,原問題等價為求使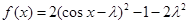 的最小值為
的最小值為 的
的 的值,這是一個二次函數與三角函數的復合函數,需分別討論以下三種情況:①
的值,這是一個二次函數與三角函數的復合函數,需分別討論以下三種情況:① ,②
,② ,③
,③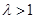 下
下 取得最小值的情況,從而可以得到
取得最小值的情況,從而可以得到 ;(3)當
;(3)當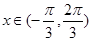 時,
時, ,
,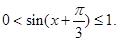 根據正弦函數
根據正弦函數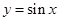 在
在 及
及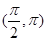 上取值的對稱性,設
上取值的對稱性,設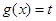 ,要保證題中方程有兩個不同的解,必須保證方程
,要保證題中方程有兩個不同的解,必須保證方程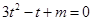 ,在
,在 僅有一根或有兩個相等根,由一元二次方程根的分布,可得
僅有一根或有兩個相等根,由一元二次方程根的分布,可得 或
或 .
.
(1)∵ ,
, ,
,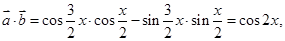
∴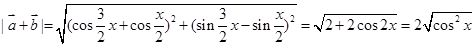
∵ , ∴
, ∴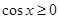 ∴
∴ 4分
4分
(2)由(1)得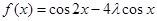 ,即
,即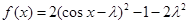
∵ , ∴
, ∴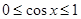
①當 時,當且僅當
時,當且僅當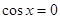 時,
時, 取得最小值
取得最小值 ,這與已知矛盾.
,這與已知矛盾.
②當 時,當且僅當
時,當且僅當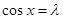 時,
時, 取最小值
取最小值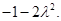
由已知得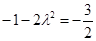 ,解得
,解得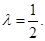
③當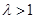 時,當且僅當
時,當且僅當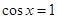 時,
時, 取得最小值
取得最小值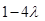 .
.
由已知得 ,解得
,解得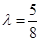 ,這與
,這與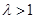 相矛盾.
相矛盾.
綜上所述, 為所求. 9分;
為所求. 9分;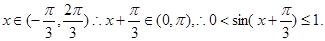 根據正弦函數
根據正弦函數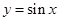 在
在 及
及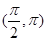 上取值的對稱性,因此設
上取值的對稱性,因此設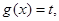 問題等價于方程
問題等價于方程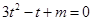 ,在
,在 僅有一根或有兩個相等根,∴
僅有一根或有兩個相等根,∴ 或
或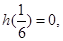 ∴
∴ 或
或
綜上, 的取值范圍是:
的取值范圍是: 或
或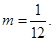 14分.
14分.
考點:1.平面向量數量積與模的坐標表示;2.二次函數與三角函數綜合;3.一元二次方程根的分布.


 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com