
設函數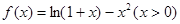 ,數列
,數列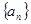 前
前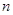 項和
項和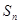 ,
,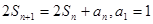 ,數列
,數列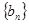 ,滿足
,滿足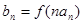 .(Ⅰ)求數列
.(Ⅰ)求數列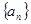 的通項公式
的通項公式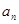 ;
;
(Ⅱ)設數列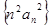 的前
的前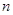 項和為
項和為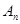 ,數列
,數列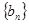 的前
的前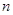 項和為
項和為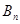 ,證明:
,證明: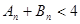 。
。
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2014屆廣東省高二第一次階段考試理科數學試卷(解析版) 題型:解答題
(本小題14分)已知點(1, )是函數
)是函數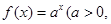 且
且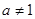 )的圖象上一點,
)的圖象上一點,
等比數列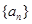 的前
的前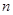 項和為
項和為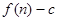 ,數列
,數列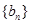
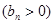 的首項為
的首項為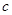 ,且前
,且前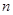 項和
項和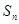 滿足
滿足
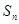 -
-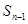 =
=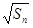 +
+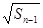 (
(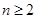 ).
).
(1)求數列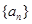 和
和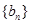 的通項公式;
的通項公式;
(2)若數列{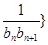 前
前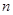 項和為
項和為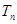 ,問
,問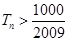 的最小正整數
的最小正整數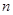 是多少?
是多少?
(3)設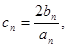 求數列
求數列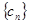 的前
的前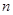 項和
項和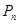
查看答案和解析>>
科目:高中數學 來源:2011-2012學年福建省高三第八次月考理科數學試卷 題型:解答題
定義函數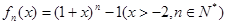 其導函數記為
其導函數記為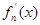 .
.
(Ⅰ)求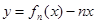 的單調遞增區間;
的單調遞增區間;
(Ⅱ)若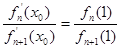 ,求證:
,求證: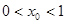 ;
;
(Ⅲ)設函數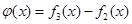 ,數列
,數列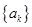 前
前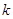 項和為
項和為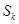 ,
, 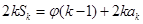 ,其中
,其中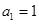 .對于給定的正整數
.對于給定的正整數 ,數列
,數列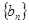 滿足
滿足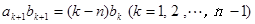 ,且
,且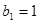 ,求
,求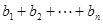 .
.
查看答案和解析>>
科目:高中數學 來源:福建省龍巖一中2011-2012學年高三下學期第八次月考試卷數學(理) 題型:解答題
定義函數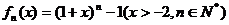 其導函數記為
其導函數記為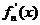 .
.
(Ⅰ)求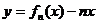 的單調遞增區間;
的單調遞增區間;
(Ⅱ)若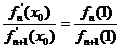 ,求證:
,求證: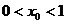 ;
;
(Ⅲ)設函數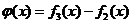 ,數列
,數列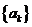 前
前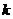 項和為
項和為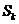 ,
,
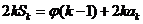 ,其中
,其中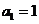 .對于給定的正整數
.對于給定的正整數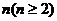 ,數列
,數列 滿足
滿足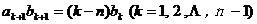 ,且
,且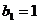 ,求
,求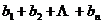 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com